题目内容
如图，架在消防车上的云梯AB长为15m，AD：BD=1：0.5，云梯底部离地面的距离BC为2m，求出云梯的顶端离地面距离AE的大小．（| 2 |
考点：解直角三角形的应用
专题：
分析：设AD=x米，由AD：BD的比值以及AB的长，利用勾股定理可建立方程，求出AD的长再加DE即BC的长，即可求出云梯的顶端离地面距离AE的大小．
解答：解：设AD=x米，
∵AD：BD=1：0.5，
∴BD=0.5x，
∵AB长为15m，
∴AD2+BD2=152，
∴x2+0.25x2=225，
解得：x=6
≈13.38米，
∴∴AE=AD+DE=13.38+2=15.38米，
∴云梯顶端离地面的距离AE为15.38米．
∵AD：BD=1：0.5，
∴BD=0.5x，
∵AB长为15m，
∴AD2+BD2=152，
∴x2+0.25x2=225，
解得：x=6
| 5 |
∴∴AE=AD+DE=13.38+2=15.38米，
∴云梯顶端离地面的距离AE为15.38米．
点评：本题考查了解直角三角形的应用，解题的关键是构造出直角三角形，将实际问题抽象成纯数学问题，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
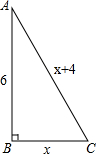求如图的Rt△ABC的面积．