题目内容
11.已知$\frac{{11-\sqrt{3}}}{3}$的整数部分为m,小数部分为n,试解方程x2+(1-m)x-(2+$\sqrt{3}$)mn=0.分析 求出$\frac{{11-\sqrt{3}}}{3}$的取值范围,确定m,n的值代入解方程即可.
解答 解:∵1$<\sqrt{3}<2$,
∴$-2<-\sqrt{3}<-1$,
∵$\frac{{11-\sqrt{3}}}{3}$=$\frac{11}{3}$$-\frac{\sqrt{3}}{3}$,
$-\frac{2}{3}$<$-\frac{\sqrt{3}}{3}$$<-\frac{1}{3}$,
∴3<$\frac{11-\sqrt{3}}{3}$<$\frac{10}{3}$,
∴m=3,n=$\frac{11}{3}$$-\frac{\sqrt{3}}{3}$-3=$\frac{2-\sqrt{3}}{3}$,
∴mn=2-$\sqrt{3}$,
∴x2+(1-m)x-(2+$\sqrt{3}$)mn=x2-2x-1
∴x2-2x-1=0
解得:${x}_{1}=\sqrt{2}+1$,x2=$-\sqrt{2}+1$.
∴方程x2+(1-m)x-(2+$\sqrt{3}$)mn=0的解为:${x}_{1}=\sqrt{2}+1$,x2=$-\sqrt{2}+1$.
点评 本题主要考查了估算无理数的大小和解一元二次方程,用夹逼法解得m,n的值是解答此题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
2.下列说法错误的是( )
| A. | 无理数是无限不循环小数 | |
| B. | 单项式-$\frac{a{b}^{2}}{3}$的系数是-$\frac{1}{3}$ | |
| C. | 近似数7.30所表示的准确数a的范围是:7.295≤a<7.305 | |
| D. | 有理数可分为整数和小数 |
 在△ABC和△DEF中,若AB=EF,∠A=∠F,增添条件可用SAS判定两三角形全等,此时∠B=∠E.
在△ABC和△DEF中,若AB=EF,∠A=∠F,增添条件可用SAS判定两三角形全等,此时∠B=∠E.
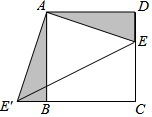 如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE'.
如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE'.