题目内容
17. 如图所示的一个圆分割成四个扇形,它们的圆心角的度数比为2:3:4:3.
如图所示的一个圆分割成四个扇形,它们的圆心角的度数比为2:3:4:3.(1)求这四个扇形的圆心角的度数,并画出四个扇形;
(2)若圆的半径为2cm,请求出这四个扇形的面积.
分析 (1)根据周角等于360°,一个圆分割成四个扇形,它们的圆心角的度数比为2:3:4:3,从而可以求得各个扇形所对的圆心角,进而可以画出四个扇形.
(2)根据扇形的面积公式即可得出结论.
解答  解:(1)如图所示,
解:(1)如图所示,
∵一个圆分割成四个扇形,它们的圆心角的度数比为2:3:4:3,
∴它们所对的圆心角分别为:
360°×$\frac{2}{12}$=60°,
360°×$\frac{3}{12}$=90°,
360°×$\frac{4}{12}$=120°,
360°×$\frac{3}{12}$=90°.
(2)∵圆的半径为2cm,
∴S1=$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π,S2=$\frac{120π×{2}^{2}}{360}$=$\frac{4}{3}$π,S3=$\frac{90π×{2}^{2}}{360}$=π,S4=$\frac{90π×{2}^{2}}{360}$=π.
点评 本题考查圆内扇形与圆的关系,关键是明确题意,进行正确分析,从而得到解答问题的方案.

练习册系列答案
相关题目
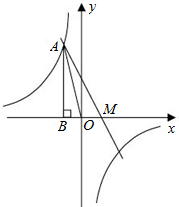 如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).
如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).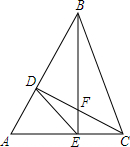 如图,△ABC中,∠A=60°,△ABC高BE、CD交于点F,下列说法中:①AD•AB=AE•AC,②BF•EF=CF•DF,③S△ABC=4S△AED,④BC=2DE,其中正确的有( )
如图,△ABC中,∠A=60°,△ABC高BE、CD交于点F,下列说法中:①AD•AB=AE•AC,②BF•EF=CF•DF,③S△ABC=4S△AED,④BC=2DE,其中正确的有( ) 如图,已知∠ACE是ABC的一个外角,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形.
如图,已知∠ACE是ABC的一个外角,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形.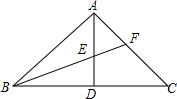 如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$. 如图,某工厂的工人师傅在一长方形铁板中挖掉一个半径为acm的圆,用代数式表示剩余部分的面积(2ab-πa2)cm2.
如图,某工厂的工人师傅在一长方形铁板中挖掉一个半径为acm的圆,用代数式表示剩余部分的面积(2ab-πa2)cm2.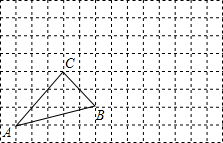 如图.把△ABC向右平移5个方格,再绕点B顺时针方向旋转90°.
如图.把△ABC向右平移5个方格,再绕点B顺时针方向旋转90°.