题目内容
 在⊙O中,CD平分∠ACB,弦AB,CD相交于点E,连接AD,BD.
在⊙O中,CD平分∠ACB,弦AB,CD相交于点E,连接AD,BD.
(1)写图中有______对相似三角形;
(2)并证明其中一对三角形相似.
解:(1)4对.
∵∠CAB=∠CDB,∠ACD=∠ABD,
∴△ACE∽△DBE,
同理:△BCE∽△DAE,
∵CD平分∠ACB,
即∠ACD=∠BCD,
∵∠ABC=∠ADC,
∴△DCA∽△BCE,
∴△DAE∽△DCA;
∴共有4对相似三角形.
故答案为:4;
(2)若选△AEC∽△DEB理由如下:
∵∠ACE=∠EBD,∠CEA=∠BED,
∴△AEC∽△DEB.
分析:(1)由圆周角定理可得∠CAB=∠CDB,∠ACD=∠ABD,然后根据有两角对应相等的三角形相似,即可判定△ACE∽△DBE,同理:△BCE∽△DAE,又由CD平分∠ACB,易判定△DCA∽△BCE,继而可得△DAE∽△DCE;
(2)选择其一,利用圆周角定理、角平分线的定义,即可证得.
点评:此题考查了相似三角形的判定与圆周角定理.此题难度适中,注意掌握数形结合思想的应用.
∵∠CAB=∠CDB,∠ACD=∠ABD,
∴△ACE∽△DBE,
同理:△BCE∽△DAE,
∵CD平分∠ACB,
即∠ACD=∠BCD,
∵∠ABC=∠ADC,
∴△DCA∽△BCE,
∴△DAE∽△DCA;
∴共有4对相似三角形.
故答案为:4;
(2)若选△AEC∽△DEB理由如下:
∵∠ACE=∠EBD,∠CEA=∠BED,
∴△AEC∽△DEB.
分析:(1)由圆周角定理可得∠CAB=∠CDB,∠ACD=∠ABD,然后根据有两角对应相等的三角形相似,即可判定△ACE∽△DBE,同理:△BCE∽△DAE,又由CD平分∠ACB,易判定△DCA∽△BCE,继而可得△DAE∽△DCE;
(2)选择其一,利用圆周角定理、角平分线的定义,即可证得.
点评:此题考查了相似三角形的判定与圆周角定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,在△ABC中,CD平分∠ACB,过D作BC的平行线交AC于M,若BC=m,AC=n,则DM=( )
如图,在△ABC中,CD平分∠ACB,过D作BC的平行线交AC于M,若BC=m,AC=n,则DM=( )A、
| ||
B、
| ||
C、
| ||
D、
|
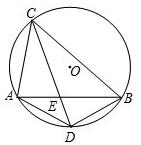 21、已知:在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连接AD、BD.
21、已知:在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连接AD、BD. 25、如图,在△ABC中,CD平分∠ACB,DE∥BC,DE=3cm,AE=2.5cm.求AC.
25、如图,在△ABC中,CD平分∠ACB,DE∥BC,DE=3cm,AE=2.5cm.求AC. 如图,在△ABC中,CD平分∠ACB,BE∥BC交AC于点E.
如图,在△ABC中,CD平分∠ACB,BE∥BC交AC于点E. 如图所示,在△ABC中,CD平分∠ACB,DE∥AC
如图所示,在△ABC中,CD平分∠ACB,DE∥AC