题目内容
解决数学问题时,我们经常要回到基本定义与基本方法思考.试利用方程的解的定义及解方程组的基本方法解决以下问题:
已知a是关于x的方程x2-(2k+1)x+4=0,及3x2-(6k-1)x+8=0的公共解,则a= ,k= .
已知a是关于x的方程x2-(2k+1)x+4=0,及3x2-(6k-1)x+8=0的公共解,则a=
考点:一元二次方程的解,一元二次方程的定义
专题:方程思想
分析:因为a是这两个方程的公共根,所以a同时满足这两个方程,把a代入这两个方程,用含k的代数式表示a,然后把a代入原方程就可以求出k的值,再求出a.
解答:解:∵a是关于x的方程x2-(2k+1)x+4=0和3x2-(6k-1)x+8=0的公共解,
∴有方程组:
①-②得:-
a+
=0,
∴a=1.
把a=1代入①有:1-(2k+1)+4=0,
解得k=2.
故答案为:a=1,k=2.
∴有方程组:
|
①-②得:-
| 4 |
| 3 |
| 4 |
| 3 |
∴a=1.
把a=1代入①有:1-(2k+1)+4=0,
解得k=2.
故答案为:a=1,k=2.
点评:本题考查的是一元二次方程的解,先设两个方程的公共解为a,得到关于a和字母系数k的方程组,解方程组就能求出a和k的值.

练习册系列答案
相关题目
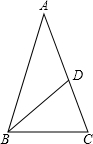 如图,在△ABC中,∠A=36°,AB=AC、BD平分∠ABC.若△ABD的周长比△BCD的周长多1厘米,则BD的长是( )
如图,在△ABC中,∠A=36°,AB=AC、BD平分∠ABC.若△ABD的周长比△BCD的周长多1厘米,则BD的长是( )| A、0.5厘米 | B、1厘米 |
| C、1.5厘米 | D、2厘米 |