题目内容
(1)分解因式:a2-2ab+b2-1;(2)解方程: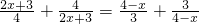 .
.
解:(1)原式=(a-b)2-1=(a-b+1)(a-b-1);
(2)设m=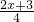 ,n=
,n= ,
,
原方程化为m+ =n+
=n+ ,即(m-n)-(
,即(m-n)-( -
- )=0,
)=0,
mn(m-n)-(m-n)=0,即(m-n)(mn-1)=0,
∴m-n=0或mn-1=0,
由m-n=0,得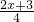 -
- =0,解得x=
=0,解得x= ,
,
由mn-1=0,得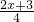 •
• -1=0,解得x1=0,x2=
-1=0,解得x1=0,x2= ,
,
经检验:原方程的解为x1=0,x2= ,x3=
,x3= .
.
分析:(1)前三项运用完全平方公式,再运用平方差公式;
(2)运用换元法.设m=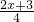 ,n=
,n= ,原方程化为m+
,原方程化为m+ =n+
=n+ ,即(m-n)-(
,即(m-n)-( -
- )=0,再通分,提公因式,得出两个方程,分别解每一个方程,结果要检验.
)=0,再通分,提公因式,得出两个方程,分别解每一个方程,结果要检验.
点评:本题考查了因式分解的方法,解分式方程的知识.当多项式的项数超过3项时,一般采用分组分解法;分式方程中,各项之间存在倒数关系时,可采用换元法解题.
(2)设m=
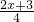 ,n=
,n= ,
,原方程化为m+
 =n+
=n+ ,即(m-n)-(
,即(m-n)-( -
- )=0,
)=0,mn(m-n)-(m-n)=0,即(m-n)(mn-1)=0,
∴m-n=0或mn-1=0,
由m-n=0,得
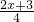 -
- =0,解得x=
=0,解得x= ,
,由mn-1=0,得
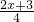 •
• -1=0,解得x1=0,x2=
-1=0,解得x1=0,x2= ,
,经检验:原方程的解为x1=0,x2=
 ,x3=
,x3= .
.分析:(1)前三项运用完全平方公式,再运用平方差公式;
(2)运用换元法.设m=
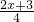 ,n=
,n= ,原方程化为m+
,原方程化为m+ =n+
=n+ ,即(m-n)-(
,即(m-n)-( -
- )=0,再通分,提公因式,得出两个方程,分别解每一个方程,结果要检验.
)=0,再通分,提公因式,得出两个方程,分别解每一个方程,结果要检验.点评:本题考查了因式分解的方法,解分式方程的知识.当多项式的项数超过3项时,一般采用分组分解法;分式方程中,各项之间存在倒数关系时,可采用换元法解题.

练习册系列答案
相关题目