题目内容
 如图,以O为圆心,半径为2的圆与反比例函数y=
如图,以O为圆心,半径为2的圆与反比例函数y= (x>0)的图象交于A、B两点,已知
(x>0)的图象交于A、B两点,已知 的长度为
的长度为 π,则k的值是
π,则k的值是
- A.

- B.

- C.2

- D.

A
分析:连接OA、OB,由弧长公式求出∠AOB的度数,过点A作AC⊥x轴,过点B作BD⊥y轴,由于点AB均在反比例函数y= 的图象上,所以BD×OD=AC×OC=k,再由OB=OA可知,BD=AC,OD=OC,故△AOC≌△BOD,由此可求出∠AOC的度数,再设A(a,b),根据锐角三角函数的定义即可求出a、b的值.
的图象上,所以BD×OD=AC×OC=k,再由OB=OA可知,BD=AC,OD=OC,故△AOC≌△BOD,由此可求出∠AOC的度数,再设A(a,b),根据锐角三角函数的定义即可求出a、b的值.
解答: 解:连接OA、OB,
解:连接OA、OB,
∵ 的长度为
的长度为 π,OA=OB=2,
π,OA=OB=2,
∴ =
= π,解得n=30°,即∠AOB=30°,
π,解得n=30°,即∠AOB=30°,
过点A作AC⊥x轴,过点B作BD⊥y轴,
∵点AB均在反比例函数y= 的图象上,
的图象上,
∴BD×OD=AC×OC=k,
∵OB=OA,
∴BD=AC,OD=OC,
∴△AOC≌△BOD,
∴∠AOC= =
= =30°,
=30°,
设A(a,b),则OC=OA•cos30°=2× =
= ,AC=b=OA×sin30°=2×
,AC=b=OA×sin30°=2× =1,
=1,
∴k=ab= ×1=
×1= .
.
故选A.
点评:本题考查的是反比例函数综合题,熟知反比例函数中k=xy的特点是解答此题的关键.
分析:连接OA、OB,由弧长公式求出∠AOB的度数,过点A作AC⊥x轴,过点B作BD⊥y轴,由于点AB均在反比例函数y=
 的图象上,所以BD×OD=AC×OC=k,再由OB=OA可知,BD=AC,OD=OC,故△AOC≌△BOD,由此可求出∠AOC的度数,再设A(a,b),根据锐角三角函数的定义即可求出a、b的值.
的图象上,所以BD×OD=AC×OC=k,再由OB=OA可知,BD=AC,OD=OC,故△AOC≌△BOD,由此可求出∠AOC的度数,再设A(a,b),根据锐角三角函数的定义即可求出a、b的值.解答:
 解:连接OA、OB,
解:连接OA、OB,∵
 的长度为
的长度为 π,OA=OB=2,
π,OA=OB=2,∴
 =
= π,解得n=30°,即∠AOB=30°,
π,解得n=30°,即∠AOB=30°,过点A作AC⊥x轴,过点B作BD⊥y轴,
∵点AB均在反比例函数y=
 的图象上,
的图象上,∴BD×OD=AC×OC=k,
∵OB=OA,
∴BD=AC,OD=OC,
∴△AOC≌△BOD,
∴∠AOC=
 =
= =30°,
=30°,设A(a,b),则OC=OA•cos30°=2×
 =
= ,AC=b=OA×sin30°=2×
,AC=b=OA×sin30°=2× =1,
=1,∴k=ab=
 ×1=
×1= .
.故选A.
点评:本题考查的是反比例函数综合题,熟知反比例函数中k=xy的特点是解答此题的关键.

练习册系列答案
相关题目




 如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.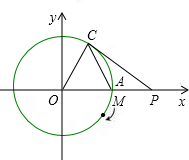 如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
 时,求动点M所经过的弧长,并写出此时M点的坐标。
时,求动点M所经过的弧长,并写出此时M点的坐标。