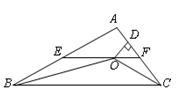
题目内容
如图，四边形ABCD与四边形AEFG都是菱形，点C在AF上，点E，G分别在BC，CD上，若∠BAD=1350，∠EAG=750，则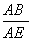
= ．
【解析】
试题分析：根据菱形的性质可得出∠BAE
=30°，∠B=45°，过点E作EM⊥AB于点M，设EM=x，则可得出AB、AE的长度，继而可得出
的值．
试题解析：∵∠BAD=135°，∠EAG=75°，四边形ABCD与四边形AEFG都是菱形，
∴∠B=180°-∠BAD=45°，∠BAE=∠BAC-∠EAC=30°，
过点E作EM⊥AB于点M，
设EM=x，在Rt△AEM中，AE=2EM=2x，AM= 
x，
在Rt△BEM中，BM=x，
则= 
．
故答案为：．
【难度】较难
练习册系列答案
阅读快车系列答案
相关题目
（x＞0）的图象经过点A（2，a）（a＞0），过点A作AB⊥x轴，垂足为点B，将线段AB沿x轴正方向平移，与反比例函数y=
；
的结果是_________.
∠A； 
