题目内容
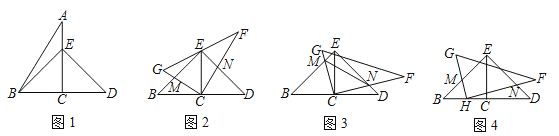
【题目】一副三角板如图1所置，其中AC边与等腰Rt△EBD斜边上的中线EC共线，以C点为旋转中心，顺时针转动△ACB，B、A两点分别于G、F两点对应，CG交BE边于点M，CF交DE边于N，已知旋转角为α，BC＝2．
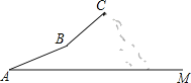
（问题发现）（1）如图2所示，若旋转角α（0°＜α＜30°）时，猜想CM与CN的数量关系，并写出你的推断过程；
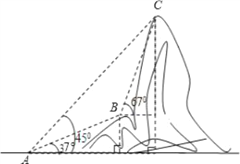
（类比探究）（2）如图3所示，若旋转角α＝75°时，（1）中的结论是否还成立？ ，此时连接MN，请直接写出MN的长度为 ；
（拓展延伸）（3）在图3的基础上将△GCF向左平移至△GHF的位置，若DH＝kBH，猜想线段HN与HM的数量关系．
【答案】（1）CM＝CN，证明详见解析；（2）成立，
；（3）HN＝kHM．
【解析】
（1）根据等腰三角形的性质得到EC⊥CD，EC＝CD＝BC，证明△BCM≌△ECN，根据全等三角形的性质证明结论；
（2）作CP⊥BE于点P，根据等腰直角三角形的性质求出PC，根据余弦的定义求出CM，根据等腰直角三角形的性质计算，得到答案；
（3）作HQ∥EC，证明△MHQ∽△NHD，根据相似三角形的性质解答即可．
解：（1）CM＝CN，
理由如下：在Rt△BED中，EB＝ED，BC＝CD，
∴EC⊥CD，EC＝CD＝BC，∠BEC＝∠DEC＝∠B＝∠D＝45°，
∵∠BCM+∠ECM＝90°，∠ECN+∠ECM＝90°，
∴∠BCM＝∠ECN，
在△BCM和△ECN中，
∴△BCM≌△ECN（ASA）
∴CM＝CN；
（2）（1）中的结论成立， 
，
理由如下：作CP⊥BE于点P，（1）中的结论成立，证明过程同（1）相同，
在Rt△BCP中，∠B＝45°，
∴PC＝BCsinB＝
，
∵∠BCM＝75°，∠BCP＝45°，
∴∠PCM＝30°，
∴CM＝
＝
，
在等腰直角三角形MCN中，MN＝PC＝，
故答案为：成立；；
（3）HN＝kHM，
理由如下：过点H作HQ∥EC交BE于点Q，
则△BHQ为等腰直角三角形，
∴BH＝HQ，
∵DH＝kBH，
∴DH＝kQH，
∵∠MHQ+∠QHF＝90°，∠NHD+∠QHF＝90°，
∴∠MHQ＝∠NHD，又∠MQH＝∠NDH，
∴△MHQ∽△NHD，
∴
＝
＝k，即HN＝kHM．
