题目内容
已知船在静水中的速度为20千米/时,水流速度为5千米/时.
(Ⅰ)若船顺水航行了t小时后又逆水航行.已知逆水比顺水多航行了5小时,求船共航行了多少千米?
(Ⅱ)若船顺水航行了S千米后又逆水航行.已知逆水与顺水航行的时间相等,逆水航行了多少千米(用含有S的式子表示)?
解:(Ⅰ)因为船顺水航行的时间为t小时,
所以逆水航行为(t+5)小时,
船共航行的路程为
(20+5)t+(20-5)(t+5)
=40t+75(千米)、
(Ⅱ)设船逆水航行了x千米,
由题意,得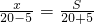 .
.
由等式的性质,得
5x=3S.
即x= .
.
逆水航行了 千米.
千米.
分析:(Ⅰ)共航行路程=顺水航行的路程+逆水航行的路程,把相关数值代入化简即可;
(Ⅱ)等量关系为:逆水航行的时间=顺水航行的时间,把相关数值代入计算即可.
点评:考查列代数式及一元一次方程的应用;根据时间相等得到等量关系是解决本题的关键;注意顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度.
所以逆水航行为(t+5)小时,
船共航行的路程为
(20+5)t+(20-5)(t+5)
=40t+75(千米)、
(Ⅱ)设船逆水航行了x千米,
由题意,得
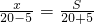 .
.由等式的性质,得
5x=3S.
即x=
 .
.逆水航行了
 千米.
千米.分析:(Ⅰ)共航行路程=顺水航行的路程+逆水航行的路程,把相关数值代入化简即可;
(Ⅱ)等量关系为:逆水航行的时间=顺水航行的时间,把相关数值代入计算即可.
点评:考查列代数式及一元一次方程的应用;根据时间相等得到等量关系是解决本题的关键;注意顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度.

练习册系列答案
相关题目
在一直线形航道上,某人乘船由A地顺流而下到B地,然后又逆流而上到C地,共乘船4h.已知船在静水中的速度为7.5km/h,水流速度为2.5km/h,若A、C两地的距离为10km,则A、B两地间的距离为( )
| A、20km | ||
B、
| ||
C、20km或
| ||
| D、以上都不正确 |