题目内容
一个正多边形的内角比它相邻的外角的4倍少20°，求这个多边形的边数．
考点：多边形内角与外角
专题：
分析：根据正多边形的性质，可得正多边形的外角相等，根据邻补角的性质，可得方程，根据解方程，可得正多边形的外角，根据多边形的外角和除以一个外角，可得答案．
解答：解；设正多边形的外角是x°，相邻的内角是（4x-20）°，由邻补角的性质，得
x+（4x-20）=180，
解得x=40．
多边形的外角和除以一个外角，得
360÷40=9，
答；这个多边形的边数是9．
x+（4x-20）=180，
解得x=40．
多边形的外角和除以一个外角，得
360÷40=9，
答；这个多边形的边数是9．
点评：本题考查了多边形的内角与外角，利用了正多边形的性质，多边形内角与外角的关系．
练习册系列答案
阅读快车系列答案
相关题目
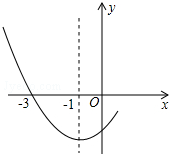如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=-1，且过点（-3，0）．下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④若（-5，y1），（