题目内容
锐角△ABC中,O,G,H分别是外心、重心、垂心.设外心到三边距离和为d外,重心到三边距离和为d重,垂心到三边距离和为d垂.
求证:1•d垂+2•d外=3•d重.
 证明:设△ABC外接圆半径为1,三个内角记为A,B,C.
证明:设△ABC外接圆半径为1,三个内角记为A,B,C.易知d外=OO1+OO2+OO3=cosA+cosB+cosC,
∴2d外=2(cosA+cosB+cosC).①
∵AH1=sinB•AB=sinB•(2sinC)=2sinB•sinC,
同样可得BH2=2sinC•sinA,CH3=2sinA•sinB.
∴3d重=△ABC三条高的和=2•(sinB•sinC+sinC•sinA+sinA•sinB) ②,
∴
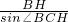 =2,
=2,∴HH1=cosC•BH=2•cosB•cosC.
同样可得HH2,HH3.
∴d垂=HH1+HH2+HH3=2(cosB•cosC+cosC•cosA+cosA•cosB) ③,
∴①+③,得1•d垂+2•d外=2(cosA+cosB+cosC)+2(cosB•cosC+cosC•cosA+cosA•cosB),
=2(cosA+cosB+cosC+cosB•cosC+cosC•cosA+cosA•cosB),
观察①、②、③,可得(cosB•cosC+cosC•cosA+cosA•cosB)+(cosA+cosB+cosC)=sinB•sinC+sinC•sinA+sinA•sinB.
则1•d垂+2•d外=3•d重.
分析:设△ABC外接圆半径为1,三个内角记为A,B,C.如图,OO1、OO2、OO3分别是O到三边的距离,利用圆心角和圆周角的关系可以得到d外=OO1+OO2+OO3=cosA+cosB+cosC;又AH1=sinB•AB,而根据正弦定理知道
 ,由此可以得到AH1=sinB•AB=sinB•(2sinC)=2sinB•sinC,接着可以得到3d重=△ABC三条高的和=2•(sinB•sinC+sinC•sinA+sinA•sinB),而,所以
,由此可以得到AH1=sinB•AB=sinB•(2sinC)=2sinB•sinC,接着可以得到3d重=△ABC三条高的和=2•(sinB•sinC+sinC•sinA+sinA•sinB),而,所以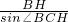 =2;由此可知HH1=cosC•BH=2•cosB•cosC,d垂=HH1+HH2+HH3=2(cosB•cosC+cosC•cosA+cosA•cosB),最后代入1•d垂+2•d外=3•d重.即可证明结论.
=2;由此可知HH1=cosC•BH=2•cosB•cosC,d垂=HH1+HH2+HH3=2(cosB•cosC+cosC•cosA+cosA•cosB),最后代入1•d垂+2•d外=3•d重.即可证明结论.点评:本题主要考查了正弦定理与余弦定理、三角形外接圆与外心,难度较大.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
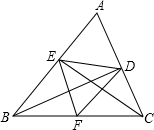 在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=
在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=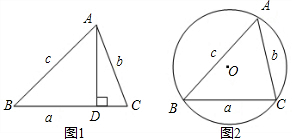
 15、已知,如图,锐角△ABC中,AD⊥BC于D,H为垂心(三角形三条高线的交点);在AD上有一点P,且∠BPC为直角.
15、已知,如图,锐角△ABC中,AD⊥BC于D,H为垂心(三角形三条高线的交点);在AD上有一点P,且∠BPC为直角.