题目内容
18.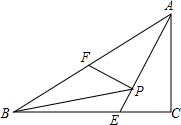 如图,在△ABC中,∠ACB=90°,AC=4,∠B=30°,F为AB的中点,AE平分∠BAC,点P为线段AE上一动点,当△BFP周长最小为4+4$\sqrt{3}$时,S△ABC=8$\sqrt{3}$.
如图,在△ABC中,∠ACB=90°,AC=4,∠B=30°,F为AB的中点,AE平分∠BAC,点P为线段AE上一动点,当△BFP周长最小为4+4$\sqrt{3}$时,S△ABC=8$\sqrt{3}$.
分析 解直角三角形求得BC,然后根据面积公式求得即可.
解答 解:∵在△ABC中,∠ACB=90°,AC=4,∠B=30°,
∴AB=8,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×4×$4\sqrt{3}$=8$\sqrt{3}$;
故答案为8$\sqrt{3}$.
点评 本题考查了解直角三角形和三角形面积,求得BC的长是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
9.某射击运动员在相同条件下的射击160次,其成绩记录如下:
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率0.8(精确到0.1).
| 射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| 射中9环以上的次数 | 15 | 33 | 48 | 63 | 79 | 97 | 111 | 130 |
| 射中9环以上的频率 | 0.75 | 0.83 | 0.80 | 0.79 | 0.79 | 0.81 | 0.79 | 0.81 |
13.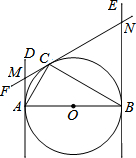 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
3.下列合并同类项中,正确的是( )
| A. | 2x+3y=5xy | B. | x2-3x2=-2x2 | C. | -2x2+2x2=x2 | D. | 3x2+2x3=5x5 |
10.下面图形中,对称轴最多的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 半圆 | D. | 等腰梯形 |
7.下列说法正确的是( )
| A. | 一个角的余角只有一个 | |
| B. | 一个角的补角必大于这个角 | |
| C. | 钝角的补角一定是锐角 | |
| D. | 若两个角互为补角,则一个是钝角,一个是锐角 |
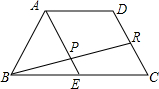 如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.
如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.