题目内容
 (2012•漳州二模)在如图所示的圆形射击靶中,所有黑、白正三角形都全等.小明向靶子射击一次,若子弹打中靶子,则子弹刚好穿过黑色区域的概率是
(2012•漳州二模)在如图所示的圆形射击靶中,所有黑、白正三角形都全等.小明向靶子射击一次,若子弹打中靶子,则子弹刚好穿过黑色区域的概率是| 1 |
| 3 |
| 1 |
| 3 |
分析:首先确定黑白两色三角形和弓形在整个圆中占的比例,根据这个比例即可求出子弹刚好穿过黑色区域的概率.
解答:解:因为黑白正三角形都全等,且黑色正三角形的个数与白正三角形的个数之比是1:2,
所以黑白正三角形的面积的和之比是1:2,
又因为黑白弓形的半径都是正三角形的边长,并且圆心角都是120°,
所以黑白两色的弓形的面积也分别相等,
因为黑白两色的弓形的个数之比是1:2,
所以黑白两色的弓形的面积的和之比是1:2,
所以黑白两色区域面积之比是1:2,
所以子弹刚好穿过黑色区域的概率是
,
故答案为:
.
所以黑白正三角形的面积的和之比是1:2,
又因为黑白弓形的半径都是正三角形的边长,并且圆心角都是120°,
所以黑白两色的弓形的面积也分别相等,
因为黑白两色的弓形的个数之比是1:2,
所以黑白两色的弓形的面积的和之比是1:2,
所以黑白两色区域面积之比是1:2,
所以子弹刚好穿过黑色区域的概率是
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查了几何概率;本题将概率的求解设置于黑白两色的正三角形和弓形中,考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 (2012•漳州二模)如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,若把四边形ABCD绕着AD边的中点O顺时针旋转90°,试解决下列问题:
(2012•漳州二模)如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,若把四边形ABCD绕着AD边的中点O顺时针旋转90°,试解决下列问题: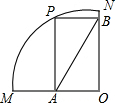 (2012•漳州二模)如图,四边形PAOB是扇形OMN的内接矩形,顶点P在
(2012•漳州二模)如图,四边形PAOB是扇形OMN的内接矩形,顶点P在