题目内容
8．
已知关于x的不等式2x-a≥-3的解集如图所示，则a的值等于（ ）| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
分析 先用a表示出x的取值范围，再由不等式的解集得出a的值即可．
解答 解：解不等式2x-a≥-3得，x≥$\frac{a-3}{2}$，
∵由图可知x≥-1，
∴$\frac{a-3}{2}$=-1，解得a=1．
故选B．
点评 本题考查的是解一元一次不等式，能根据题意得出不等式的解集是解答此题的关键．
练习册系列答案
相关题目
19．若$\sqrt{x+3}$+|y-2|=0，则$\sqrt{x^y}$=（ ）
| A． | -3 | B． | 3 | C． | ±3 | D． | $2\sqrt{2}$ |
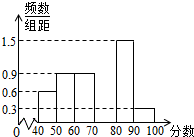某校从参加计算机测试的学生中抽取了60名学生的成绩（40～100分）进行分析，并将其分成了六段后绘制成如图所示的频数分布直方图（其中70～80段因故看不清），若60分以上（含60分）为及格，试根据图中信息来估计这次测试的及格率约为75%．
19．已知a＜b，下列不等式中，变形正确的是（ ）
| A． | a-3＞b-3 | B． | $\frac{a}{3}$＞$\frac{b}{3}$ | C． | 3a-1＞3b-1 | D． | -3a＞-3b |
15．
如图，OC平分∠AOB，OD平分∠AOC，∠AOD=35°，则∠AOB等于（ ）
如图，OC平分∠AOB，OD平分∠AOC，∠AOD=35°，则∠AOB等于（ ）| A． | 80° | B． | 100° | C． | 110° | D． | 140° |