题目内容
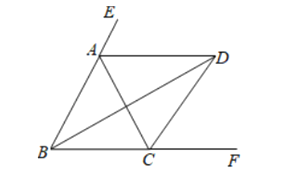
【题目】如图，等腰直角三角形
中，
，
.先将
绕点
逆时针方向旋转
，得到
，点
对应点
，点
对应点
；再将沿
方向平移，得到
，点、、的对应点分别是点
、
、
，设平移的距离为
，且
．
（1）在图中画出和；
（2）记
与
的交点为点
，
与
的交点为点
，如果四边形
的面积是
的面积的3倍，试求四边形
和
的面积的比值．
【答案】（1）见解析 （2）3
【解析】
（1）根据作法将AB、AC分别逆时针旋转90°可得AB1、AC1，连接B1C1即可得
；将沿
方向平移，得到
，因为平移的距离为
，且
，故要注意C2在线段C1A上；
（2）根据旋转的性质先证四边形AC1B1C是正方形，再根据四边形
的面积是
的面积的3倍求得D为AC的中点，利用三角形是全等进行转化即可．
（1）如图，和就是所求的三角形．
（2）连接B1C，如图：
由题意可得：∠CAC1=∠C1=90°，CB=CA=C1A=C1B1
∴AC∥B1C1
∴四边形AC B1C1是平行四边形
又∠C1=90°，CA=C1A
∴四边形AC B1C1是正方形
∴
90°
∴B1、C、B三点共线，B1C∥AC1
∴B2在B1C上
∵四边形的面积是的面积的3倍
∴四边形AC B2C2的面积是的面积的4倍
即
∴AC=2CD，AD=CD
又
90°，
∴
∴
∴矩形
的面积=矩形
的面积
又
90°，
∴
∴
的面积是四边形AC B2C2的面积的
，即为矩形的面积的
∴四边形
是的面积的3倍
∴四边形和的面积的比值为3 ．
阅读快车系列答案
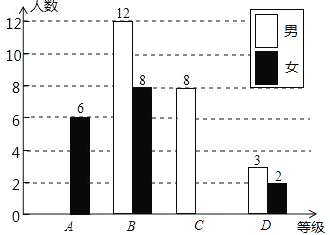
【题目】)6月5日是世界环境日，某校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成如下统计图：
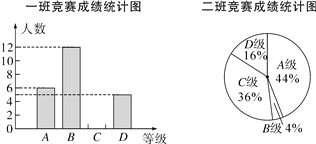
根据以上提供的信息解答下列问题：
(1)把一班竞赛成绩统计图补充完整；
(2)写出下表中a，b，c的值：
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面对这次竞赛成绩的结果进行分析：
①从平均数和中位数方面比较一班和二班的成绩；
②从平均数和众数方面比较一班和二班的成绩；
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩．
