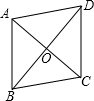
题目内容
对角线长为a的正方形的面积为________．
分析：由对角线可求得边长的大小，进而可求得面积．
解答：∵对角线长为a
∴边长为
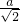，即面积为
a2．故答案为
a2．点评：掌握正方形边长与对角线的比为1：
，在以后的做题中可直接运用． 
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
如图，用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为
如图，用一块直径为1m的圆桌布平铺在对角线长为1m的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、2-
|
