Question

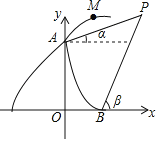
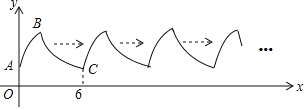
【题目】如图，曲线AB是顶点为B，与y轴交于点A的抛物线y＝﹣x2+4x+2的一部分；曲线BC是双曲线y＝的一部分．由点C开始不断重复“A﹣B﹣C”的过程，形成一组波浪线，点P（2018，m）与Q（2026，n）均在该抛物线上，则m+n＝_____．

Answer 1

【答案】9

【解析】

依据题意可得，A，C之间的水平距离为6，点Q与点P的水平距离为8，A，B之间的水平距离为2，双曲线解析式为y＝，依据点P'、点B离x轴的距离相同，都为6，即点P的纵坐标m＝6，点Q″、点Q'离x轴的距离相同，都为3，即点Q的纵坐标n＝3，即可得到m+n的值．

由图可得，A，C之间的水平距离为6，

2018÷6＝336…2，

由抛物线y＝﹣x2+4x+2可得，顶点B（2，6），即A，B之间的水平距离为2，

∴点P'、点B离x轴的距离相同，都为6，即点P的纵坐标m＝6，

由抛物线解析式可得AO＝2，即点C的纵坐标为2，

∴C（6，2），

∴k＝2×6＝12，

∴双曲线解析式为y=，

2026﹣2018＝8，故点Q与点P的水平距离为8，

∵点P'、Q″之间的水平距离＝（2+8）﹣（2+6）＝2，

∴点Q″的横坐标＝2+2＝4，

∴在y＝中，令x＝4，则y＝3，

∴点Q″、点Q'离x轴的距离相同，都为3，即点Q的纵坐标n＝3，

∴m+n＝6+3＝9，

故答案为：9．