Question

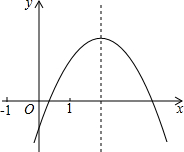二次函数y=ax²+bx+c的图象如图所示，给出下列结论：①ac＞0；②2|b|＞|a+c|；③b²-4ac≥0；④b+2a＞c，其中正确的结论是

 

．

Answer 1

考点：二次函数图象与系数的关系

专题：

分析：根据图象首先判断出a+b+c＞0，进而分别判断a，c的符号，再利用图象与x轴交点个数以及对称轴方程，即可得出答案．

解答：解：由图象可得出：当x=1时，a+b+c＞0，
∵图象开口向下，则a＜0，
∵图象与y轴交于y轴负半轴，则c＜0，
∴①ac＞0，此选项正确；
②∵a＜0，c＜0，a+b+c＞0，
∴b＞|a+c|，
∴2|b|＞|a+c|，故此选项正确；
③∵图象与x轴有两个交点，∴b²-4ac＞0，此选项错误；
④∵对称轴方程为：x=-

b

2a

＞1，
∴-b＜2a，
∴2a+b＞0，
∵c＜0，
∴b+2a＞c，故此选项正确．
故答案为：①②④．

点评：此题主要考查了二次函数图象与系数的关系，得出a+b+c以及-

b

2a

的符号是解题关键．