Question

11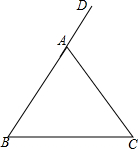．如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角，AM是∠DAC的平分线，AC的垂直平分线与AM交于点F，与BC边交于点E，连接AE、CF．
（1）补全图形；
（2）判断四边形AECF的形状并加以证明．

Answer 1

分析 （1）画出图形；
（2）先证明AF∥EC，再利用△AOF≌△COE，证明AF=CE，所以四边形AECF是平行四边形，又因为EF是AC的垂直平分线，所以四边形AECF是菱形．

解答 解：（1）如图所示：
（2）猜想：四边形AECF是菱形，
证明：∵AB=AC，AM平分∠CAD，
∴∠B=∠ACB，∠CAD=2∠CAM，
∵∠CAD是△ABC的外角，
∴∠CAD=∠B+∠ACB，
∴∠CAD=2∠ACB，
∴∠CAM=∠ACB，
∴AF∥CE，
∴∠FAO=∠ACE
∵EF垂直平分AC，
∴OA=OC，∠AOF=∠COF=90°，
∴△AOF≌△COE，
∴AF=CE，
在四边形AECF中，AF∥CE，AF=CE，
∴四边形AECF是平行四边形，
又∵EF⊥AC，
∴四边形AECF是菱形．

点评 本题既考查了复杂作图，又考查了线段垂直平分线、等腰三角形及菱形的性质和判定，熟练掌握菱形的判定方法是关键，常用的方法有：①一组邻边相等的平行四边形是菱形，②对角线互相垂直的平行四边形是菱形，③四条边都相等的四边形是菱形．