题目内容
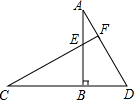如图，AB⊥CD于B，CF交AB于E，CE=AD，BE=BD，求证：CF⊥AD．
证明：在Rt△CBE和Rt△ABD中
，
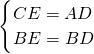∴Rt△CBE≌Rt△ABD （HL），
∴∠C=∠A，
∵∠AEF=∠CEB，
∴∠CBE=∠AFE=90°，
∴CF⊥AD．
分析：根据HL定理求出Rt△CBE≌Rt△ABD，进而得出∠C=∠A，即可得出∠CBE=∠AFE=90°，进而得出答案．
点评：此题主要考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理得出是解题关键．
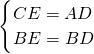，∴Rt△CBE≌Rt△ABD （HL），
∴∠C=∠A，
∵∠AEF=∠CEB，
∴∠CBE=∠AFE=90°，
∴CF⊥AD．
分析：根据HL定理求出Rt△CBE≌Rt△ABD，进而得出∠C=∠A，即可得出∠CBE=∠AFE=90°，进而得出答案．
点评：此题主要考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理得出是解题关键．
练习册系列答案
相关题目
16、如图，AB⊥CD于点O，EF经过点O，∠COF=4∠BOF．求∠COF和∠BOE的度数．
2、如图，AB⊥CD于点O，EF经过O点，且∠EOB=36°，则∠BOF的度数为（ ）
如图，AB⊥CD于B，△ABD和△BCE都是等腰直角三角形，如果CD=17，BE=5，那么AC的长为（ ）
如图，AB⊥CD于点O，EF为过点O的一条直线，若∠1=55°，则∠2=
如图，AB⊥CD于点O，EF经过点O，∠1=28°，∠COF=