题目内容
15.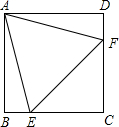 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEF=75°;③BE+DF=EF;④${S_{正方形ABCD}}=2+\sqrt{3}$;⑤$tan∠AEB=2+\sqrt{3}$,其中正确的( )个.
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEF=75°;③BE+DF=EF;④${S_{正方形ABCD}}=2+\sqrt{3}$;⑤$tan∠AEB=2+\sqrt{3}$,其中正确的( )个.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 根据三角形的全等的知识可以判断①正确;等边三角形的每个内角=60°判断②不正确;根据线段垂直平分线的知识可以判断③不正确;利用勾股定理求正方形边长得出面积等知识可以判断④正确;利用锐角三角函数得出⑤正确.
解答 解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=60°,
∴②不正确;
∵在Rt△ABE和Rt△ADF中,$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴①正确;
如图,连接AC,交EF于G点,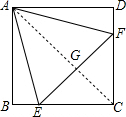
∴AC⊥EF,且AC平分EF,
∵∠CAD≠∠CAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③不正确;
∵EF=2,
∴CE=CF=$\sqrt{2}$,
设正方形的边长为a,
在Rt△ADF中,
a2+(a-$\sqrt{2}$)2=4,
解得a=$\frac{\sqrt{2}±\sqrt{6}}{2}$(负值舍去),
∴a=$\frac{\sqrt{2}+\sqrt{6}}{2}$
则a2=2+$\sqrt{3}$,
∴S正方形ABCD=2+$\sqrt{3}$,
④说法正确;
∵a-$\sqrt{2}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$,
∴tan∠AEB=$\frac{\frac{\sqrt{6}+\sqrt{2}}{2}}{\frac{\sqrt{6}-\sqrt{2}}{2}}$=2+$\sqrt{3}$,
∴⑤正确;
∴正确的有①④⑤.
故选C.
点评 本题主要考查正方形的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理以及锐角三角函数的知识;解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题有一定难度.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案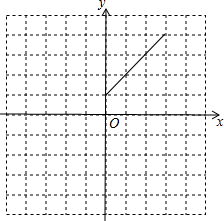 我们知道,把直线y=x向左平移1个单位可得到一次函数y=x+1的图象,把直线y=kx(k≠0)向左平移1个单位可得到一次函数y=k(x+1)的图象,把抛物线y=ax2(a≠0)向左平移1个单位,可得到二次函数y=a(x+1)2的图象.
我们知道,把直线y=x向左平移1个单位可得到一次函数y=x+1的图象,把直线y=kx(k≠0)向左平移1个单位可得到一次函数y=k(x+1)的图象,把抛物线y=ax2(a≠0)向左平移1个单位,可得到二次函数y=a(x+1)2的图象.类似的:我们将函数y=|x|向左平移1个单位,在平面直角坐标系中画出了新函数的部分图象,请回答下列问题:
(1)平移后的函数解析式是y=|x+1|;
(2)借助下列表格,用你认为最简单的方法补画平移后的函数图象:
| x | … | … | ||||||
| y | … | … |
| A. | 全等三角形的对应边相等,对应角相等 | |
| B. | 全等三角形的对应边上的中线相等 | |
| C. | 两条边和一个角对应相等的两个三角形全等 | |
| D. | 全等三角形的面积相等 |
 如图,在山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,则山高AB=50$\sqrt{3}$+50米.
如图,在山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,则山高AB=50$\sqrt{3}$+50米. 如图所示,已知OB⊥OA,直线CD过点O,且∠AOC=35°,则∠BOD=125°.
如图所示,已知OB⊥OA,直线CD过点O,且∠AOC=35°,则∠BOD=125°.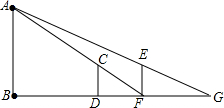 如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小华在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小华的身高为1.5m,求路灯杆AB的高度.
如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小华在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小华的身高为1.5m,求路灯杆AB的高度.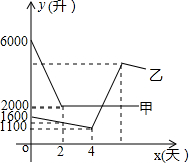 随着哈尔滨汽车的增加,哈市某乙储油库的储油量一直以每天相同的速度持续减少.为保证用户用油量,大庆某甲储油库立即以管道运输方式向哈市的乙储油库输油2天.如图,是两储油库的储油量y(升)与时间x(天)之间的函数图象.在单位时间内,甲储油库的放油量与乙储油库的进油量相同(油在排放、接收以及输送过程中的损耗不计).下列四种说法:
随着哈尔滨汽车的增加,哈市某乙储油库的储油量一直以每天相同的速度持续减少.为保证用户用油量,大庆某甲储油库立即以管道运输方式向哈市的乙储油库输油2天.如图,是两储油库的储油量y(升)与时间x(天)之间的函数图象.在单位时间内,甲储油库的放油量与乙储油库的进油量相同(油在排放、接收以及输送过程中的损耗不计).下列四种说法: