题目内容
6. 在△ABC中,∠C=90°,AC=BC,D是AB的中点,∠EDF=90°
在△ABC中,∠C=90°,AC=BC,D是AB的中点,∠EDF=90°(1)求证:EC=FB;
(2)试探究线段AE+BF与EF的大小关系;
(3)求证:四边形ECFD的面积是△ABC的面积的一半;
(4)若E、F为AC、BC边上的动点,其他条件不变,则(1)、(2)、(3)中的结论是否仍然成立?
分析 (1)连接CD,证明△CED与△BFD全等即可证得EC=FB;
(2)通过证△CED≌△BFD,EC=FB,同理证得△AED≌△CFD,AE=CF.在△CEF中,CE+CF>EF,所以FB+AE>EF;
(3)由(2)中的结论不难得到△CED的面积=△BFD面积,△AED的面积=△CFD的面积,所以四边形ECFD的面积是△ABC的面积的一半;
(4)由(1)、(2)、(3)的证明过程可说明,若E、F为AC、BC边上的动点,其他条件不变,(1)、(2)、(3)中的结论仍然成立.
解答 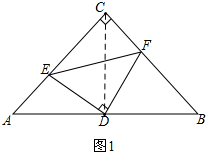 解:(1)连接CD,如图1,
解:(1)连接CD,如图1,
∵∠C=90°,AC=BC,D是AB的中点,
∴CD⊥AB,CD=AD=BD,∠ACD=∠BCD=∠CAB=∠CBA=45°,(等腰三角形底边上的高线、顶角的平分线与底边的中线互相重合),
∵∠EDF=90°,
∴∠EDC=∠FDB(同角的余角相等),
在△EDC和△FDB中,
$\left\{\begin{array}{l}{∠EDC=∠FDB}\\{CD=BD}\\{∠ECD=∠FBD}\end{array}\right.$,
∴△EDC≌△FDB(ASA),
∴EC=FB(全等三角形的对应边相等);
(2)由(1)中△EDC≌△FDB的证明,同理可证得△AED≌△CFD
∴AE=CF(全等三角形对应边相等),
又∵EC=FB,
在△CEF中,EC+CF>EF,
∴AE+FB>EF;
(3)∵△CED≌△BFD,△AED≌△CFD,
∴S△CED=S△BFD,S△AED=S△CFD,
∴S△CED+S△CFD=S△BFD+S△AED,
即:S四边形ECFD=S△BFD+S△AED,
∴四边形ECFD的面积是△ABC的面积的一半;
(4)若E、F为AC、BC边上的动点,其他条件不变,则(1)、(2)、(3)中的结论仍然成立.
点评 对于等腰三角形的问题,常常应用“三线合一”这条性质,即:等腰三角形底边上的中线、顶角的平分线、底边上的高线互相重合,解决本题的关键是引出辅助线:中线CD.

| A. | 4x-5=3x+2 变形得 4x-3x=2-5 | B. | $\frac{2}{3}$x=$\frac{3}{2}$变形得x=1 | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{x-1}{2}$=$\frac{x}{5}$变形得3x=5 |
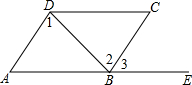 如图,已知AD∥BC,下列结论不一定正确的是( )
如图,已知AD∥BC,下列结论不一定正确的是( )| A. | ∠A+∠ABC=180° | B. | ∠1=∠2 | C. | ∠A=∠3 | D. | ∠C=∠3 |
| A. | 29.3×107 | B. | 2.93×108 | C. | 0.293×1010 | D. | 2.93×109 |
 如图,△ABC中,分别以AB、AC为边向外作正方形ABDE、ACFG.试说明:
如图,△ABC中,分别以AB、AC为边向外作正方形ABDE、ACFG.试说明: