题目内容
如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=OC.

证明见解析.
【解析】
试题分析:根据等边对等角可得∠ABC=∠ACB,然后利用“角角边”证明△BCE和△CBD全等,根据全等三角形对应角相等可得∠BCE=∠CBD,再利用等角对等边即可得证.
试题解析:∵AB=AC,
∴∠ABC=∠ACB,
∵BD⊥AC,CE⊥AB,
∴∠BDC=∠CEB=90°,
在△BCE和△CBD中,
 ,
,
∴△BCE≌△CBD(AAS),
∴∠BCE=∠CBD,
∴BO=CO.
考点:1.等腰三角形的判定与性质;2.全等三角形的判定与性质.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
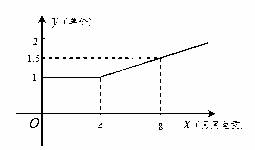
 x刻画.
x刻画.
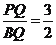 ;③S△PDQ=
;③S△PDQ=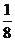 ;④cos∠ADQ=
;④cos∠ADQ=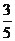 .其中正确结论是_________.(填写序号)
.其中正确结论是_________.(填写序号)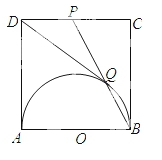

 ∠B=
∠B=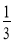 ∠C ④∠A=∠B=2∠C ⑤∠A=∠B=
∠C ④∠A=∠B=2∠C ⑤∠A=∠B= ∠C 中能确定△ABC为直角三角形的条件有( ).
∠C 中能确定△ABC为直角三角形的条件有( ).