题目内容
在下列条件中①∠A+∠B=∠C ②∠A﹕∠B﹕∠C=1﹕2﹕3 ③∠A= ∠B=
∠B=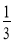 ∠C ④∠A=∠B=2∠C ⑤∠A=∠B=
∠C ④∠A=∠B=2∠C ⑤∠A=∠B= ∠C 中能确定△ABC为直角三角形的条件有( ).
∠C 中能确定△ABC为直角三角形的条件有( ).
A.2个 B.3个 C.4个 D.5个
C.
【解析】
试题分析:根据三角形内角和定理,结合已知条件可分别求出各角的度数,然后作出判断.因为∠A+∠B+∠C=180°,所以若①∠A+∠B=∠C,则∠C=90°,三角形是直角三角形;②∠A﹕∠B﹕∠C=1﹕2﹕3,则∠A=30°,∠B=60°,∠C=90°,三角形为直角三角形; ③∠A= ∠B=
∠B= ∠C,∠A=30°,∠B=60°,∠C=90°,三角形为直角三角形;④∠A=∠B=2∠C,则∠A=∠B=72°,∠C=36°,三角形不是直角三角形;⑤∠A=∠B=
∠C,∠A=30°,∠B=60°,∠C=90°,三角形为直角三角形;④∠A=∠B=2∠C,则∠A=∠B=72°,∠C=36°,三角形不是直角三角形;⑤∠A=∠B= ∠C,∠A=∠B=45°,∠C=90°.
∠C,∠A=∠B=45°,∠C=90°.
故选:C.
考点:三角形内角和定理.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 的解是
的解是 
 的解集为
的解集为 ,则
,则 的值为( )
的值为( ) D.
D.
 ,
, ,求32m-3n+1的值.
,求32m-3n+1的值.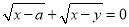 (a>0)
(a>0)
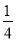 .
.