Question

【题目】已知正反比例函数的图像交于、两点，过第二象限的点作轴，点的横坐标为，且，点在第四象限

（1）求这两个函数解析式；

（2）求这两个函数图像的交点坐标；

（3）若点在坐标轴上，联结、，写出当时的点坐标

Answer 1

【答案】（1）y=-，y=（2）A（-2，3），B（2，-3）（3）（2，0）或（-2，0）或（0，3）或（0，-3）

【解析】

（1）先根据题意得出，再结合知，再利用待定系数法求解可得；（2）联立正反比例函数解析式得到方程组，解之即可得交点坐标；（3）由“点在坐标轴上”分点在轴上和轴上两种情况，根据利用割补法求解可得．

解：（1）如图，

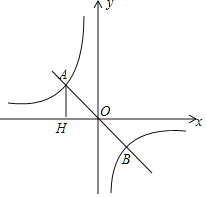
∵点的横坐标为-2，且轴，

∴，

∵，

∴，

则点，

将代入得：，则正比例函数的解析式为；

将代入得：，则反比例函数的解析式为；

（2）∵

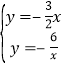
∴得：或，

∵点在第四象限，

∴点坐标为，

故答案为：.

（3）若在轴上，设，

∵

∴，

解得：或，

∴点的坐标为或；

若在轴上，设，

∵

∴，

解得：或，

∴点的坐标为或；

综上，点的坐标为或或或．