题目内容
在四边形ABCD中，AB∥CD，∠D=900,∠DCA=300,CA平分∠DCB，AD=4cm,求AB的长度.
过点B作BE⊥AC,垂足为E.
∵AB∥CD，∴∠BAC=∠DCA=30°.
∵CA平分∠DCB，∴∠ACB=∠DCA=30°.
∴∠BAC=∠BCA.∴AB=BC.∴CE=
AC.
∵∠D=900,∠DCA=300, AD=4cm,∴AC=8cm.∴CE=4cm.
在Rt△CEB中，设BE=X,则BC=2X,根据勾股定理可得（2x）2－x2=42.解得
.
∴
.
∵AB∥CD，∴∠BAC=∠DCA=30°.
∵CA平分∠DCB，∴∠ACB=∠DCA=30°.
∴∠BAC=∠BCA.∴AB=BC.∴CE=
AC.∵∠D=900,∠DCA=300, AD=4cm,∴AC=8cm.∴CE=4cm.
在Rt△CEB中，设BE=X,则BC=2X,根据勾股定理可得（2x）2－x2=42.解得
.∴
.利用平行线+角平分线构造等腰三角形，利用含有30°角的直角三角形的边角关系求得AB的长.
练习册系列答案
优质课堂快乐成长系列答案
相关题目
中，
，
，
，且
，
的度数；（2）四边形
的面积（结果保留根号）；
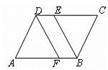
沿EF折叠，使点
落在
边上的点B处；沿BG折叠，使点
落在点D处，且BD过F点.
，
，
，
，点
在
上，
，
是
中点，在
上找一点
使
的值最小，此时其最小值一定等于（ ）
ABCD中，AC与BD交于点O，点E是BC边的中点，OE=1,则AB的长是 .