题目内容
如图，a∥b，AB⊥a于点D，BC交直线b于点E，若∠1=43°，则∠2的度数是
- A.137°
- B.133°
- C.120°
- D.100°
B
分析：先作辅助线延长AB交直线b于点F，再利用平行线的性质和三角形外角和内角的关系求角的度数．
解答：延长AB交直线b于点F
∵a∥b，AB⊥a，
∴AB⊥b，
∴∠BFE=90°；
∵∠1=43°，∠2是三角形BEF的一个外角，
∴∠2=∠BFE+∠1=90°+43°=133°．
故选B．
点评：构造三角形是常用的作辅助线的方法．
分析：先作辅助线延长AB交直线b于点F，再利用平行线的性质和三角形外角和内角的关系求角的度数．
解答：延长AB交直线b于点F
∵a∥b，AB⊥a，
∴AB⊥b，
∴∠BFE=90°；
∵∠1=43°，∠2是三角形BEF的一个外角，
∴∠2=∠BFE+∠1=90°+43°=133°．
故选B．
点评：构造三角形是常用的作辅助线的方法．
练习册系列答案
相关题目
6、如图所示，直线AB、CD相交于点O，作∠DOE=∠BOD，OF平分∠AOE，若∠AOC=20°，则∠EOF=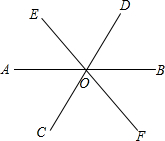
如图，三条直线AB、CD、EF相交于同一点O，若∠AOE=2∠AOC，∠COF=60°，求∠BOD的度数．
22、（初三）如图，△ABC中，AB=AC，I为△ABC的内心，AI的延长线交△ABC的外接圆于点D，过点I作BC的平行线分别交AB、AC于E、F，若O是△DEF外接圆的圆心．
（1）解不等式组：