12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是20;
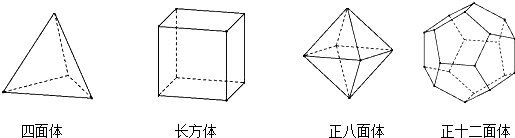
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 8 | 12 | |
| 正十二面体 | 20 | 12 | 30 |
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是20;

10.观察图中每一个大三角形中白色的三角形的排列规律,则第5个大三角形中白色的三角形有( )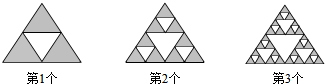

| A. | 82个 | B. | 154 | C. | 83个 | D. | 121个 |
5.
0 162099 162107 162113 162117 162123 162125 162129 162135 162137 162143 162149 162153 162155 162159 162165 162167 162173 162177 162179 162183 162185 162189 162191 162193 162194 162195 162197 162198 162199 162201 162203 162207 162209 162213 162215 162219 162225 162227 162233 162237 162239 162243 162249 162255 162257 162263 162267 162269 162275 162279 162285 162293 199269
| 口算. 33×30= | 3500÷7= | 10×70= | 20×60= | 30×4= | 1500÷5= |
| 4×21= | 400÷5= | 96÷3= | 34÷2= | 720-8= | 30×50= |
| 300÷5= | 24×3= | 20×20= |