题目内容
一个圆柱和一个圆锥的底面半径之比是2:3,体积之比是3:2,它们高的比是
- A.1:3
- B.3:4
- C.9:8
C
分析:根据“一个圆柱和一个圆锥的底面半径之比是2:3,体积之比是3:2,”把圆柱的底面半径看作2份,圆锥的底面半径是3份,圆柱的体积是3份,圆锥的体积是2份;再根据圆柱与圆锥的体积公式,分别得出圆柱与圆锥的高的求法,进而得出答案.
解答:因为,V=πr2h,
所以,h=V÷(πr2),
=3÷(4π)=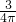 ,
,
因为V= πr2h,
πr2h,
所以h=3V÷(πr2),
=2×3÷(9π),
=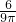 ,
,
=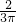 ,
,
圆柱与圆锥的高的比: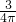 :
: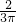 =9:8;
=9:8;
故选:C.
点评:由于是求两个数的比,所以把对应的量看作份数,另外在计算时π不用代入数据.
分析:根据“一个圆柱和一个圆锥的底面半径之比是2:3,体积之比是3:2,”把圆柱的底面半径看作2份,圆锥的底面半径是3份,圆柱的体积是3份,圆锥的体积是2份;再根据圆柱与圆锥的体积公式,分别得出圆柱与圆锥的高的求法,进而得出答案.
解答:因为,V=πr2h,
所以,h=V÷(πr2),
=3÷(4π)=
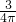 ,
,因为V=
 πr2h,
πr2h,所以h=3V÷(πr2),
=2×3÷(9π),
=
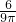 ,
,=
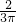 ,
,圆柱与圆锥的高的比:
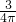 :
: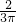 =9:8;
=9:8;故选:C.
点评:由于是求两个数的比,所以把对应的量看作份数,另外在计算时π不用代入数据.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目