题目内容
(2004?武汉)一个圆柱和一个圆锥的体积之比是8:3,圆柱底面半径是圆锥底面半径的2倍.若圆锥的高是36厘米,则圆柱的高是
8
8
厘米.分析:根据等底等高的圆锥的体积是圆柱体积的
,已知个圆柱和一个圆锥的体积之比是8:3,圆柱底面半径是圆锥底面半径的2倍,又知道圆锥的高是36厘米,求圆柱的高是多少厘米.根据它们的体积公式,设圆锥的底面半径为r,则圆柱的底面半径为2r,圆柱的高为h,根据比的意义解答.
| 1 |
| 3 |
解答:解:设圆锥的底面半径为r,则圆柱的底面半径为2r,圆柱的高为h,
由题意得:圆柱的体积:圆锥的体积=8:3;
[π×(2r)2×h]:[
πr2×36]=8:3;
[π×4r2×h]:[πr2×12]=8:3;
化简得:h:3=8:3;
即h=8;
答:圆柱的高是8厘米.
故答案为:8.
由题意得:圆柱的体积:圆锥的体积=8:3;
[π×(2r)2×h]:[
| 1 |
| 3 |
[π×4r2×h]:[πr2×12]=8:3;
化简得:h:3=8:3;
即h=8;
答:圆柱的高是8厘米.
故答案为:8.
点评:此题主要根据圆柱和圆锥的体积计算方法以及运用等底等高的圆柱和圆锥体积之间的关系解决问题.

练习册系列答案
相关题目
 (2004?武汉)胡裁缝加工一批服装的情况如图.已知他加工一件童装、一条裤子和一件上衣所需要时间的比是1:2:3,他每天加工2件童装、3条裤子和4件上衣.请问,他加工完这批服装用了多少天?
(2004?武汉)胡裁缝加工一批服装的情况如图.已知他加工一件童装、一条裤子和一件上衣所需要时间的比是1:2:3,他每天加工2件童装、3条裤子和4件上衣.请问,他加工完这批服装用了多少天?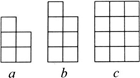 (2004?武汉)有一些大小相同的正方体木块堆成一堆,从上往下看是图a,从前往后看是图b,从左往右看是图c,这堆木块至少有
(2004?武汉)有一些大小相同的正方体木块堆成一堆,从上往下看是图a,从前往后看是图b,从左往右看是图c,这堆木块至少有