题目内容
如图所示，已知ABCD是长方形，
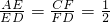，求三角形ABE与三角形DEF的面积之比．
解：设长方形的长为a，宽为b，则AB=b，AE=
a，DE=
a，DF=b，
S△ABE=a×b×
=
ab；
S△DEF=a×b×=
ab；
S△ABE：S△DEF=ab：ab=3：4；
答：三角形ABE与三角形DEF的面积之比为3：4．
分析：设长方形的长为a，宽为b，则AB=b，AE=a，DE=a，DF=b，分别用a和b，依据三角形的面积公式表示出三角形ABE与三角形DEF的面积，进而求出其面积之比．
点评：解答此题的关键是：分别用长方形的长和宽表示出两个三角形的面积，即可求其面积比．
a，DE=a，DF=b，S△ABE=
a×b×=ab；S△DEF=
a×b×=ab；S△ABE：S△DEF=
ab：ab=3：4；答：三角形ABE与三角形DEF的面积之比为3：4．
分析：设长方形的长为a，宽为b，则AB=b，AE=
a，DE=a，DF=b，分别用a和b，依据三角形的面积公式表示出三角形ABE与三角形DEF的面积，进而求出其面积之比．点评：解答此题的关键是：分别用长方形的长和宽表示出两个三角形的面积，即可求其面积比．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
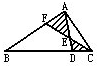如图所示，已知S△ABC=1，FE=EC，AF=
如图所示，已知阴影部分的面积为4.5平方厘米，求三角形ABC的面积．
如图所示，已知三角形ABC的面积是平行四边形CDEF面积的3倍，AD=2DC，且三角形BDE的面积为3，则三角形BEF的面积为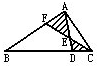
如图所示，已知S△ABC=1，FE=EC，AF=
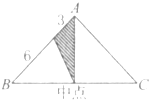如图所示，已知阴影部分的面积为4.5平方厘米，求三角形ABC的面积．