题目内容
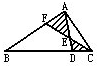 如图所示,已知S△ABC=1,FE=EC,AF=
如图所示,已知S△ABC=1,FE=EC,AF=| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
分析:先过E点作AB的平行线,GH交AC于H点,GH交BC于G点,再根据S△EDC=S△ECH=S△AEH,从把要求的阴影部分的面积转化到了一个大的梯形AFEH中,然后根据梯形的面积公式进行计算,计算过程中是用字母表示长度的,从而找出了梯形面积和大三角形ABC的关系,最后根据S△ABC=1整体代入,从而求出阴影部分的面积.
解答:解:过E点作AB的平行线,GH交AC于H点,GH交BC于G点,如下图所示:
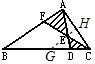
因为GH平行于AB,且FE=EC,所以EH=
AF,AH=
AC,
可见:S△EDC=S△ECH=S△AEH,
所以阴影部分的面积等于梯形AFEH的面积,
根据题意知S△ABC=1,所以:AB×h÷2=1,
S阴=S梯AFEH=(
AB+
AB÷2)×
h÷2,
=
AB×
h÷2,
=
(AB×h÷2),
=
×1,
=
,
故答案为:
.

因为GH平行于AB,且FE=EC,所以EH=
| 1 |
| 2 |
| 1 |
| 2 |
可见:S△EDC=S△ECH=S△AEH,
所以阴影部分的面积等于梯形AFEH的面积,
根据题意知S△ABC=1,所以:AB×h÷2=1,
S阴=S梯AFEH=(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:此题的关键一是作辅助线后,用字母代入公式计算,二是把S△ABC=1整体代入,这是本题的两个难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 甲、乙两位同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s (km)和骑行时间f(h)之间的关系如图所示.给出下列说法:
甲、乙两位同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s (km)和骑行时间f(h)之间的关系如图所示.给出下列说法: 甲、乙两位同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s (km)和骑行时间f(h)之间的关系如图所示.给出下列说法:
甲、乙两位同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s (km)和骑行时间f(h)之间的关系如图所示.给出下列说法: