题目内容
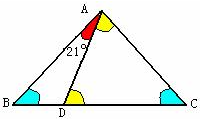 如图,在三角形ABC中,点D在BC上,且∠ABC=∠ACB、∠ADC=∠DAC,∠DAB=21°,求∠ABC的度数;并回答:图中哪些三角形是锐角三角形.
如图,在三角形ABC中,点D在BC上,且∠ABC=∠ACB、∠ADC=∠DAC,∠DAB=21°,求∠ABC的度数;并回答:图中哪些三角形是锐角三角形.分析:因为三角形的内角和是180度,所以∠DAC+∠ADC+∠C=180°,而∠DAC=∠ADC=∠B+21,∠B=∠C,所以3×∠B+21°=180°,然后求出∠B的度数,进而求出∠DAC和∠BAC的度数,继而判断出图中哪些三角形是锐角三角形.
解答: 解:因为∠DAC+∠ADC+∠C=180°,
解:因为∠DAC+∠ADC+∠C=180°,
而∠DAC=∠ADC=∠B+21,
∠B=∠C,
所以3×∠B+21°=180°,
因为∠B=46°;
∠DAC=46°+21°=67°,∠BAC=67°+21°=88°,
所以△ABC和△ADC都是锐角三角形.
 解:因为∠DAC+∠ADC+∠C=180°,
解:因为∠DAC+∠ADC+∠C=180°,而∠DAC=∠ADC=∠B+21,
∠B=∠C,
所以3×∠B+21°=180°,
因为∠B=46°;
∠DAC=46°+21°=67°,∠BAC=67°+21°=88°,
所以△ABC和△ADC都是锐角三角形.
点评:熟记三角形的外角关系和内角和定理以及理清思路是解决此题的关键;用到的知识点:三角形的分类.

练习册系列答案
相关题目
 如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( )
如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( ) 如图:在三角形ABC中,BD=
如图:在三角形ABC中,BD= 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍.
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍. 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的 如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.
如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.