题目内容
如图，在三角形ABC中，BD：DC=1：2，AE=ED，则AF：FC=（ ）分析：过点D作AC的平行线交BF与G，然后根据相似三角形的性质解出答案．
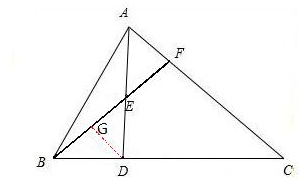
解答：解：过点D作AC的平行线交BF与G，
所以△BDG与△BCF相似，△AEF与△DEG相似
所以
=
=
=
，
=
因为AE=DE，
所以DG=AF，
所以
=
即AF：CF=1：3；
故选：B．
所以△BDG与△BCF相似，△AEF与△DEG相似
所以
| DG |
| CF |
| BD |
| BC |
| 1 |
| 1+2 |
| 1 |
| 3 |
| AE |
| DE |
| AF |
| DG |
因为AE=DE，
所以DG=AF，
所以
| AF |
| CF |
| 1 |
| 3 |
故选：B．
点评：解题的关键是作平行线，然后利用相似三角形的性质解答．
练习册系列答案
相关题目
如图：在三角形ABC中，BD=
如图，在三角形ABC中，CD的长是BD长的2倍，E是AC的中点，则三角形ABC的面积是三角形ADE面积的（ ） 倍．
如图，在三角形ABC中，CD的长是BD长的2倍，E是AC的中点，则三角形ABC的面积是三角形ADE面积的
如图，在三角形ABC中，D、E为两个三等分点，F为AB的中点，若△EDF的面积是12平方厘米，则△ABC的面积是（ ）平方厘米．