题目内容
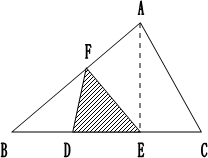
 如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.
如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.分析:连接AE,因为D、E是三等分点,根据三角形的高一定时,三角形的面积与底的成正比例的性质可得,三角形ABE的面积=
三角形ABC的面积=三角形BFE的面积×2=三角形EDF的面积×4,因为三角形EDF的面积是12平方厘米,由此代入即可解决问题.
| 2 |
| 3 |

解答:解:连接AE,因为D、E是三等分点,F是中点,所以三角形ABE的面积=
三角形ABC的面积=三角形BFE的面积×2=三角形EDF的面积×4,
则三角形ABC的面积是:12×4÷
=72(平方厘米),
答:三角形ABC的面积是72平方厘米.
故选:C.
| 2 |
| 3 |
则三角形ABC的面积是:12×4÷
| 2 |
| 3 |
答:三角形ABC的面积是72平方厘米.
故选:C.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( )
如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( ) 如图:在三角形ABC中,BD=
如图:在三角形ABC中,BD= 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍.
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍. 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的