题目内容
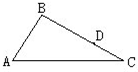 如图,有一条三角形的环路,A至B是上坡路.B至C是下坡路,A至C是平路,A至B、B至C、A至C三段距离的比是3:4:5.心怡和爱琼同时从A出发,心怡按顺时针方向行走,爱琼按逆时针方向行走,2小时半后在BC上D点相遇.已知两人上坡速度是4千米/小时,下坡速度是6千米/小时,在平路上速度是5千米/小时.求C至D是多少千米.
如图,有一条三角形的环路,A至B是上坡路.B至C是下坡路,A至C是平路,A至B、B至C、A至C三段距离的比是3:4:5.心怡和爱琼同时从A出发,心怡按顺时针方向行走,爱琼按逆时针方向行走,2小时半后在BC上D点相遇.已知两人上坡速度是4千米/小时,下坡速度是6千米/小时,在平路上速度是5千米/小时.求C至D是多少千米.分析:由于三段距离的比为是3:4:5,所以可设AB长3x(km),BC长4x(km),AC长5x(km),则心怡走BD所用的时间为:2.5-3x÷4,爱琼走DC所用时间为:2.5-5x÷5,由此可得方程:6×(2.5-3x÷4)+4×(2.5-5x÷5)=4x,解此方程,然后再据距离时间求出CD之间的距离即可.
解答:解:设AB长3x(km),BC长4x(km),AC长5x(km),可得方程:
6×(2.5-3x÷4)+4×(2.5-5x÷5)=4x
(15-
x)+(10-x)=4x,
25-8
x=4x,
x=2;
则CD之间的距离为:
(2.5-5x÷5)×4
=0.5×4,
=2(千米).
答:C至D是2千米.
6×(2.5-3x÷4)+4×(2.5-5x÷5)=4x
(15-
| 9 |
| 2 |
25-8
| 1 |
| 2 |
x=2;
则CD之间的距离为:
(2.5-5x÷5)×4
=0.5×4,
=2(千米).
答:C至D是2千米.
点评:本题根据三条边的长度比及时间、距离、路程之间的基本关系列方程解答比较简单.

练习册系列答案
相关题目
 一块直角梯形土地的对角线上有一条小路(如图),把这块土地分成了两个三角形.已知梯形的上底、下底分别是16米和23米,高12米.这块梯形的面积是多少?
一块直角梯形土地的对角线上有一条小路(如图),把这块土地分成了两个三角形.已知梯形的上底、下底分别是16米和23米,高12米.这块梯形的面积是多少? 如图,有边长分别是15分米和20分米的两个正方形,一条直线把这两个相连的正方形分成甲、乙、丙、丁四部分.甲三角形的面积比丙三角形的面积大多少平方分米?
如图,有边长分别是15分米和20分米的两个正方形,一条直线把这两个相连的正方形分成甲、乙、丙、丁四部分.甲三角形的面积比丙三角形的面积大多少平方分米?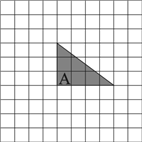 如图,在正方形网格中画有一个不等腰的直角三角形A.若再贴上一个三角形B,使所得的图形是等腰三角形,但要求三角形B与三角形A除了有一条公共边重合外,没有其他的公共点,那么,符合条件的三角形B有
如图,在正方形网格中画有一个不等腰的直角三角形A.若再贴上一个三角形B,使所得的图形是等腰三角形,但要求三角形B与三角形A除了有一条公共边重合外,没有其他的公共点,那么,符合条件的三角形B有 阅读以下两则材料,并完成后面的4个问题.
阅读以下两则材料,并完成后面的4个问题.