题目内容
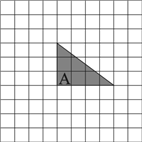 如图,在正方形网格中画有一个不等腰的直角三角形A.若再贴上一个三角形B,使所得的图形是等腰三角形,但要求三角形B与三角形A除了有一条公共边重合外,没有其他的公共点,那么,符合条件的三角形B有
如图,在正方形网格中画有一个不等腰的直角三角形A.若再贴上一个三角形B,使所得的图形是等腰三角形,但要求三角形B与三角形A除了有一条公共边重合外,没有其他的公共点,那么,符合条件的三角形B有7
7
个.(三角形B的顶点要在格子点上)分析:根据题意进行分析可知:以原三角形的边长4,5为腰画出即可与新三角形一起组成一个等腰三角形即有6个,作原来斜边的中垂线,并与边长为3的直角边的延长线交于一点,此点与原三角形斜边两点构成的三角形也符合要求,从而得出结论共有7个符合要求的三角形.
解答:解:如图所示:
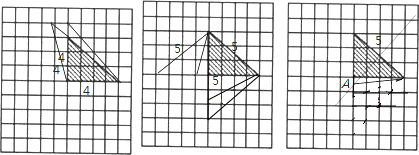
因为根据题意可知:
以4为腰的等腰三角形有2个,以5为腰的三角形有4个,以5为腰的等腰三角形有1个,
所以符合要求的新三角形有2+4+1=7个.
故答案为:7.

因为根据题意可知:
以4为腰的等腰三角形有2个,以5为腰的三角形有4个,以5为腰的等腰三角形有1个,
所以符合要求的新三角形有2+4+1=7个.
故答案为:7.
点评:本题主要考查了等腰三角形的定义,同时需要认真分析,避免遗漏,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
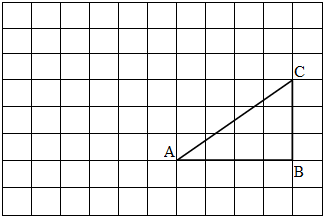
 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.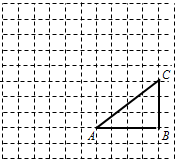 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
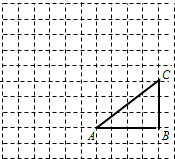
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1. 如图,正方形网格中,△ABC是格点三角形,将△ABC绕点A按逆时针方向旋转90゜得到△AB1C1.
如图,正方形网格中,△ABC是格点三角形,将△ABC绕点A按逆时针方向旋转90゜得到△AB1C1.