题目内容
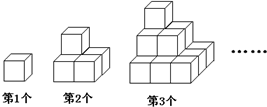 如图,第1个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体叠放而成的.按照这样的规律继续叠放下去,第7个图形中,从正面看,看得到的木块应有
如图,第1个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体叠放而成的.按照这样的规律继续叠放下去,第7个图形中,从正面看,看得到的木块应有28
28
块,看不到的木块应有112
112
块.分析:解答此题应根据图,找出规律:第1个图形小正方体的个数是1,第,2个图形小正方体的个数是12+22=4个,第3个图形小正方体的个数是12+22+32=14个,依次类推进行解答即可.
解答:解:①第7个图形中木块的总数是12+22+32+42+52+62+72=140(块);
②第7个图形中看得到的块数是:1+2+3+4+5+6+7=28(块);
③第7个图形中看不到的块数是:140-28=112(块);
②第7个图形中看得到的块数是:1+2+3+4+5+6+7=28(块);
③第7个图形中看不到的块数是:140-28=112(块);
点评:解答此题的关键是先找出规律,进而根据规律进行解答即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

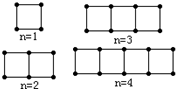 (2007?淮安模拟)如图,由火柴棒拼出的一列图形中,第n个图形由n个正方形组成.通过观察可以发现:
(2007?淮安模拟)如图,由火柴棒拼出的一列图形中,第n个图形由n个正方形组成.通过观察可以发现: 如图,由火柴棒拼出的一列图形中,第n个图形由n个正方形组成.通过观察可以发现:
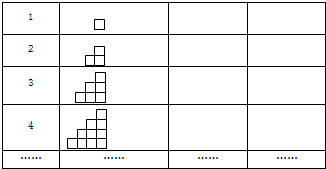
如图,由火柴棒拼出的一列图形中,第n个图形由n个正方形组成.通过观察可以发现: 如图,第(1)个图有1个黑球;第(2)个图为3个同样大小球叠成的图形,最下一层的2个球为黑色,其余为白色;第(3)个图为6个同样大小球叠成的图形,最下一层的3个球为黑色,其余为白色…则从第(n)个图中随机取出一个球,是黑球的可能性是______.
如图,第(1)个图有1个黑球;第(2)个图为3个同样大小球叠成的图形,最下一层的2个球为黑色,其余为白色;第(3)个图为6个同样大小球叠成的图形,最下一层的3个球为黑色,其余为白色…则从第(n)个图中随机取出一个球,是黑球的可能性是______.