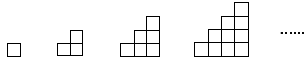题目内容
把边长为1cm的正方形如图那样一层、两层、三层…拼成图形.先填表,再解答下面的问题.
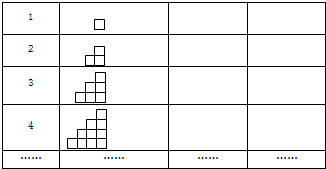
(1)第n个图形的周长是多少厘米?
(2)第n个图形的面积是多少平方厘米?
(3)一个图形的周长是40厘米,这个图形的面积是多少平方厘米?

(1)第n个图形的周长是多少厘米?
(2)第n个图形的面积是多少平方厘米?
(3)一个图形的周长是40厘米,这个图形的面积是多少平方厘米?
分析:(1)首先注意摆放的方式.计算其周长时,注意找个起点,再回到这个起点.
(2)(3)第n个图形有n层,小正方形的个数一共有:1+2+3+…+n个,每个小正方形的面积是1平方厘米,据此即可求出它的面积.
(2)(3)第n个图形有n层,小正方形的个数一共有:1+2+3+…+n个,每个小正方形的面积是1平方厘米,据此即可求出它的面积.
解答:解:(1)一层时的周长是:1×4=4(厘米);
两层时的周长是:2+1+1+1+1+2=8(厘米);
三层时的周长是:3+1+1+1+1+1+1+3=12(厘米);
四层时的周长是:4+1+1+1+1+1+1+1+1+4=16(厘米);
它们的周长组成的数列是4,8,12,16,…它们的周长是层数×4厘米;
当n层时周长就是n×4=4n(厘米).
(2)(1+2+3+…+n)×1×1=
(平方厘米),
答:第n个图形的面积是
平方厘米.
(3)当4n=40时,
n=10,
所以面积是:
=55(平方厘米),
答:它的面积是55平方厘米.
两层时的周长是:2+1+1+1+1+2=8(厘米);
三层时的周长是:3+1+1+1+1+1+1+3=12(厘米);
四层时的周长是:4+1+1+1+1+1+1+1+1+4=16(厘米);
它们的周长组成的数列是4,8,12,16,…它们的周长是层数×4厘米;
当n层时周长就是n×4=4n(厘米).
(2)(1+2+3+…+n)×1×1=
| n(n+1) |
| 2 |
答:第n个图形的面积是
| n(n+1) |
| 2 |
(3)当4n=40时,
n=10,
所以面积是:
| 10(10+1) |
| 2 |
答:它的面积是55平方厘米.
点评:关键是通过归纳与总结,得到其中的规律.注意由特殊到一般的归纳方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 判断推理.把边长为1cm的正方形如图这样一层、两层、三层…通过摆放,拼成各种图形.你能发现其中的规律吗?看图找出规律,并填写表格.
判断推理.把边长为1cm的正方形如图这样一层、两层、三层…通过摆放,拼成各种图形.你能发现其中的规律吗?看图找出规律,并填写表格.
| 层数 | 1层 | 2层 | 3层 | 4层 | n层 |
| 个数 | 1个 | 3个 | 6个 |
 (2012?汨罗市模拟)判断推理.把边长为1cm的正方形如图这样一层、两层、三层…通过摆放,拼成各种图形.你能发现其中的规律吗?看图找出规律,并填写表格.
(2012?汨罗市模拟)判断推理.把边长为1cm的正方形如图这样一层、两层、三层…通过摆放,拼成各种图形.你能发现其中的规律吗?看图找出规律,并填写表格. (2008?金坛市)把边长为1cm的正方形如下图那样一层、两层、三层…拼成各种图形.
(2008?金坛市)把边长为1cm的正方形如下图那样一层、两层、三层…拼成各种图形.