题目内容
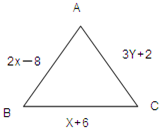 已知三角形ABC为等边三角形,其三边长如下图所示,求
已知三角形ABC为等边三角形,其三边长如下图所示,求| X2-Y2 |
| X2+2Y2 |
| 27 |
| 40 |
分析:根据等边三角形的性质可得方程2x-8=x+6,解方程求出x=14;再根据等边三角形的性质可得方程3y+2=14+6,解方程求出y;再将x,y的值代入
×1
,计算即可求解.
| X2-Y2 |
| X2+2Y2 |
| 27 |
| 40 |
解答:解:根据题意有:
2x-8=x+6,
2x-x=6+8,
x=14;
3y+2=14+6,
3y+2-2=14+6-2,
3y=18,
y=6.
把 x=14,y=6代入
×1
,
原式=
×
,
=
×
,
=1.
答:
×1
的值为1.
2x-8=x+6,
2x-x=6+8,
x=14;
3y+2=14+6,
3y+2-2=14+6-2,
3y=18,
y=6.
把 x=14,y=6代入
| X2-Y2 |
| X2+2Y2 |
| 27 |
| 40 |
原式=
| 142-62 |
| 142+2×62 |
| 67 |
| 40 |
=
| 40 |
| 67 |
| 67 |
| 40 |
=1.
答:
| X2-Y2 |
| X2+2Y2 |
| 27 |
| 40 |
点评:考查了等边三角形的性质,解方程及含字母式子的求值,本题的关键是得到关于x,y的方程,求得x,y的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14)
已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14) 已知三角形ABC为等边三角形,其三边长如下图所示,求
已知三角形ABC为等边三角形,其三边长如下图所示,求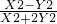 ×1
×1 的值.
的值.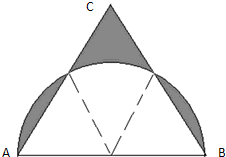 已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14)
已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14) ×1
×1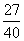 的值。
的值。