题目内容
 如图,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L形区域乙和丙.已知三块区域甲、乙、丙的周长之比4:5:7,并且区域丙的面积为48,求大正方形的面积.
如图,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L形区域乙和丙.已知三块区域甲、乙、丙的周长之比4:5:7,并且区域丙的面积为48,求大正方形的面积.
解:周长之比就等于边长之比,设甲、乙、丙的边长为4a,5a,7a
49a2-25a2=48,
a2=2;
大正方形的面积:49a2=98;
答:大正方形的面积是98.
分析:周长之比就等于边长之比,设甲、乙、丙的边长为4a,5a,7a;根据“正方形的面积=边长×边长”分别求出大正方形和中正方形的面积,然后根据“大正方形的面积-中正方形的面积=丙的面积”列出方程,求出a2=2;进而求出大正方形的面积.
点评:解答此题的关键:根据题意,设出甲、乙、丙的边长,进而根据正方形的面积计算公式分别求出大正方形和中正方形的面积,然后根据大正方形的面积、中正方形的面积和丙的面积三者之间的关系列出方程,求出a2=2;进而求出大正方形的面积.
49a2-25a2=48,
a2=2;
大正方形的面积:49a2=98;
答:大正方形的面积是98.
分析:周长之比就等于边长之比,设甲、乙、丙的边长为4a,5a,7a;根据“正方形的面积=边长×边长”分别求出大正方形和中正方形的面积,然后根据“大正方形的面积-中正方形的面积=丙的面积”列出方程,求出a2=2;进而求出大正方形的面积.
点评:解答此题的关键:根据题意,设出甲、乙、丙的边长,进而根据正方形的面积计算公式分别求出大正方形和中正方形的面积,然后根据大正方形的面积、中正方形的面积和丙的面积三者之间的关系列出方程,求出a2=2;进而求出大正方形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
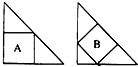 在一个给定的等腰三角形中画内接正方形,有两种画法(如图).则正方形A与正方形B的面积比为
在一个给定的等腰三角形中画内接正方形,有两种画法(如图).则正方形A与正方形B的面积比为 如图,在一个4×4的正方形内,两个
如图,在一个4×4的正方形内,两个 在边长2dm的正方形内(如图)画一个最大的圆,并用字母标出圆的圆心和半径,然后计算出所画圆的面积是这个正方形面积的百分之几?
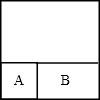
在边长2dm的正方形内(如图)画一个最大的圆,并用字母标出圆的圆心和半径,然后计算出所画圆的面积是这个正方形面积的百分之几? 如图,在大正方形内有一个小正方形A和一个长方形B,它们的面积比是2:3.那么,大正方形和小正方形的面积比是________.
如图,在大正方形内有一个小正方形A和一个长方形B,它们的面积比是2:3.那么,大正方形和小正方形的面积比是________.