题目内容
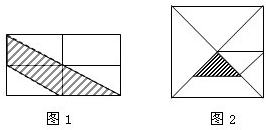
先观察图1中的阴影部分占长方形面积的 .在仿照图1的思考方法,分一分,回答:在图2的七巧板图形中,阴影部分的面积占整个图形面积的
.在仿照图1的思考方法,分一分,回答:在图2的七巧板图形中,阴影部分的面积占整个图形面积的
解:(1)作出长方形的另一条对角线,
则长方形被8等分,
阴影部分占了3份,
所以阴影部分的面积占总面积的 .
.
(2)图二中,阴影部分的面积与三角形①的面积相等,
又因三角形①的面积是三角形ABC面积的 ,
,
三角形ABC 的面积又是正方形面积的 ,
,
所以阴影部分的面积占总面积的 ×
× =
= .
.
答:图一中阴影部分的面积占总面积的 ,
,
图二中,阴影部分的面积占总面积的 .
.
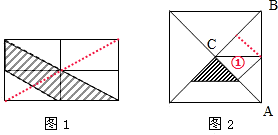
分析:如图所示,由题意可知:图一中,可以看作是将长方形8等分,则阴影部分占长方形面积的 ,而图二中,阴影部分的面积与三角形①的面积相等,又因三角形①的面积是三角形ABC面积的
,而图二中,阴影部分的面积与三角形①的面积相等,又因三角形①的面积是三角形ABC面积的 ,三角形ABC 的面积又是正方形面积的
,三角形ABC 的面积又是正方形面积的 ,于是可以求出阴影部分的面积占正方形的面积的几分之几.
,于是可以求出阴影部分的面积占正方形的面积的几分之几.
点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半,等底等高的三角形的面积相等.
则长方形被8等分,
阴影部分占了3份,
所以阴影部分的面积占总面积的
 .
.(2)图二中,阴影部分的面积与三角形①的面积相等,
又因三角形①的面积是三角形ABC面积的
 ,
,三角形ABC 的面积又是正方形面积的
 ,
,所以阴影部分的面积占总面积的
 ×
× =
= .
.答:图一中阴影部分的面积占总面积的
 ,
,图二中,阴影部分的面积占总面积的
 .
.分析:如图所示,由题意可知:图一中,可以看作是将长方形8等分,则阴影部分占长方形面积的
 ,而图二中,阴影部分的面积与三角形①的面积相等,又因三角形①的面积是三角形ABC面积的
,而图二中,阴影部分的面积与三角形①的面积相等,又因三角形①的面积是三角形ABC面积的 ,三角形ABC 的面积又是正方形面积的
,三角形ABC 的面积又是正方形面积的 ,于是可以求出阴影部分的面积占正方形的面积的几分之几.
,于是可以求出阴影部分的面积占正方形的面积的几分之几.
点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半,等底等高的三角形的面积相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
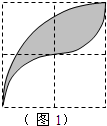 已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.
已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.
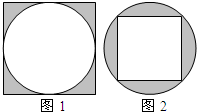 如图1、2,两个圆的半径相等,设图1中的阴影部分面积为S1,图2中的阴影部分面积为S2,那么S1与S2之间的大小关系为( )
如图1、2,两个圆的半径相等,设图1中的阴影部分面积为S1,图2中的阴影部分面积为S2,那么S1与S2之间的大小关系为( )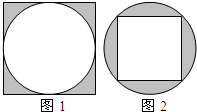 如图1、2,两个圆的半径相等,设图1中的阴影部分面积为S1,图2中的阴影部分面积为S2,那么S1与S2之间的大小关系为
如图1、2,两个圆的半径相等,设图1中的阴影部分面积为S1,图2中的阴影部分面积为S2,那么S1与S2之间的大小关系为