题目内容
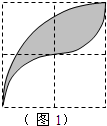 已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.
已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.(1)填空:图1中阴影部分的面积是
π-2
π-2
(结果保留π);(2)请你在下图中以图1为基本图案,借助轴对称、平移或旋转设计一个完整的花边图案(要求至少含有两种图形变换).

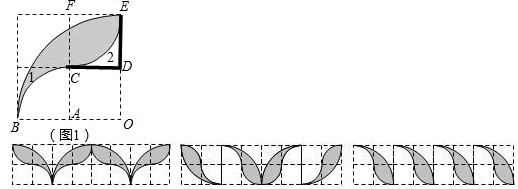
分析:(1)如下图所示,阴影部分的面积=扇形OBE的面积-正方形OACD的面积-扇形ABC的面积-弧CE与CD,DE围成图形的面积.
弧CE与CD,DE围成图形的面积=小正方形EFCD的面积-扇形FCE的面积,据此即可求解;
(2)借助轴对称、平移或旋转即可解决问题.
弧CE与CD,DE围成图形的面积=小正方形EFCD的面积-扇形FCE的面积,据此即可求解;
(2)借助轴对称、平移或旋转即可解决问题.
解答:解:(1)如图:则阴影部分的面积为
-1×1-
-(1×1-
),
=π-1-
-1+
=π-2;
(2)所设计方案如下图所示:
 .
.
| 90×π×22 |
| 360 |
| 90×π×12 |
| 360 |
| 90×π×12 |
| 360 |
=π-1-
| π |
| 4 |
| π |
| 4 |
=π-2;
(2)所设计方案如下图所示:
 .
.点评:解决本题的关键是弄清图中的扇形的半径与圆心,把不规则的图形的面积转化为几个规则图形的面积的和或差来求解.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
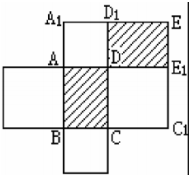 长方形ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积之和是68平方米,求长方形ABCD的面积.(已将辅助图形画好)
长方形ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积之和是68平方米,求长方形ABCD的面积.(已将辅助图形画好) 如图,大正方形的一个顶点A落在小正方形的中心,已知大、小正方形的边长分别是19厘米和10厘米,求重叠部分的面积.
如图,大正方形的一个顶点A落在小正方形的中心,已知大、小正方形的边长分别是19厘米和10厘米,求重叠部分的面积. 长方形ABCD的周长为16米,在它的每条边上各画一个以该边为边的正方形(如图),已知这四个正方形的和是68平方米,则长方形ABCD的面积是
长方形ABCD的周长为16米,在它的每条边上各画一个以该边为边的正方形(如图),已知这四个正方形的和是68平方米,则长方形ABCD的面积是