题目内容
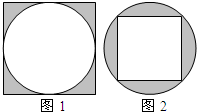如图1、2，两个圆的半径相等，设图1中的阴影部分面积为S1，图2中的阴影部分面积为S2，那么S1与S2之间的大小关系为（ ）分析：图1中，正方形的边长就等于圆的直径，阴影部分的面积=正方形的面积-圆的面积；图2中，正方形的对角线就等于圆的直径，从而可以求正方形的面积，阴影部分的面积=圆的面积-正方形的面积，据此即可比较两图中阴影部分的面积的大小．
解答：解：设圆的半径为r，
则S1=（2r）2-πr2，
=（4-π）r2，
=0.86r2；
S2=πr2-2r×r÷2×2，
=πr2-2r2，
=（π-2）r2
=1.14r2；
所以S1＜S2．
故答案为：A．
则S1=（2r）2-πr2，
=（4-π）r2，
=0.86r2；
S2=πr2-2r×r÷2×2，
=πr2-2r2，
=（π-2）r2
=1.14r2；
所以S1＜S2．
故答案为：A．
点评：解答此题的关键是：利用已知条件分别表示出阴影部分的面积，进而即可比较其大小．
练习册系列答案
相关题目
仔细观察如图1所示的两个圆，并回答问题．
（1）画出图中互相垂直的两条对称轴．
如图．在带箭头和刻度的射线上依次作100个圆（相邻两圆的半径相差1厘米）．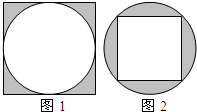
如图1、2，两个圆的半径相等，设图1中的阴影部分面积为S1，图2中的阴影部分面积为S2，那么S1与S2之间的大小关系为