题目内容
 如图,两个正方形的边长分别是8厘米和10厘米,求图中阴影部分的面积.
如图,两个正方形的边长分别是8厘米和10厘米,求图中阴影部分的面积.
解:CG∥EF,所以△BCH和△BEF相似,
因为CE=EF=10厘米,BC=8厘米,
即BC:BE=8:(10+8),
所以CH:EF=8:(10+8),
CH:10=8:(8+10),
CH=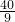 (厘米);
(厘米);
阴影部分的面积= ×底×高=
×底×高= ×8×
×8×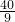 =
=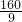 (平方厘米);
(平方厘米);
答:图中阴影部分的面积是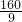 平方厘米.
平方厘米.
分析:在正方形CEFG中,因为CG∥EF,所以△BCH和△BEF相似,因为CE=EF=10厘米,BC=8厘米,即BC:BE=8:(10+8),所以CH:EF=8:(10+8),由此即可求得CH的长度,再根据三角形的面积公式即可求出阴影部分的面积.
点评:此题考查了相似三角形的对应边成比例的性质的灵活应用.
因为CE=EF=10厘米,BC=8厘米,
即BC:BE=8:(10+8),
所以CH:EF=8:(10+8),
CH:10=8:(8+10),
CH=
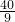 (厘米);
(厘米);阴影部分的面积=
 ×底×高=
×底×高= ×8×
×8×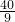 =
=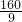 (平方厘米);
(平方厘米);答:图中阴影部分的面积是
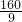 平方厘米.
平方厘米.分析:在正方形CEFG中,因为CG∥EF,所以△BCH和△BEF相似,因为CE=EF=10厘米,BC=8厘米,即BC:BE=8:(10+8),所以CH:EF=8:(10+8),由此即可求得CH的长度,再根据三角形的面积公式即可求出阴影部分的面积.
点评:此题考查了相似三角形的对应边成比例的性质的灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
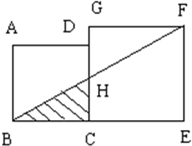 (2012?仙游县模拟)如图,两个正方形的边长分别是8厘米和10厘米,求图中阴影部分的面积.
(2012?仙游县模拟)如图,两个正方形的边长分别是8厘米和10厘米,求图中阴影部分的面积.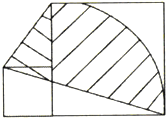 如图,两个正方形的边长分别是4厘米和10厘米,求阴影部分的面积.
如图,两个正方形的边长分别是4厘米和10厘米,求阴影部分的面积.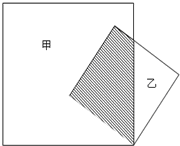 如图,两个正方形的边长分别为10厘米和7厘米,甲、乙两块空白区域的面积之和为87平方厘米,那么阴影部分的面积是
如图,两个正方形的边长分别为10厘米和7厘米,甲、乙两块空白区域的面积之和为87平方厘米,那么阴影部分的面积是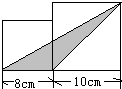 如图,两个正方形的边长分别是8厘米和10厘米,阴影部分的面积是
如图,两个正方形的边长分别是8厘米和10厘米,阴影部分的面积是 如图,两个正方形的边长分别是6厘米、4厘米,阴影部分的面积是
如图,两个正方形的边长分别是6厘米、4厘米,阴影部分的面积是