题目内容
(1)3,5,7,9,11…________(第30个);
(2) ,
, ,
, ,
, ,
, ,
, ,…________(第100个);
,…________(第100个);
(3) ,
,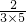 ,
,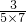 ,
,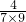 ,
,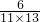 ,
,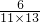 …________(第10个);
…________(第10个);
(4)1=1=1×1
1+3=4=2×2
1+3+5+7=16=4×4
1+3+5+7+9+11+13=________=________×________
1+3+5+7+9+11+13+…________=________=50×50.
解:由分析得出:
(1)3,5,7,9,11…61;(第30个);
(2) ,
, ,
, ,
, ,
, ,
, ,…
,… (第100个);
(第100个);
(3) ,
,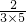 ,
,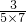 ,
,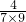 ,
,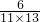 ,
,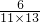 …
…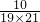 (第10个);
(第10个);
(4)1=1=1×1
1+3=4=2×2
1+3+5+7=16=4×4
1+3+5+7+9+11+13=49=7×7;
1+3+5+7+9+11+13+…99=2500=50×50.
故答案为:(1)61;(2) ;(3)
;(3)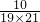 ;(4)49,7,7;99,2500.
;(4)49,7,7;99,2500.
分析:(1)数列中的数依次增加2,所以第30个数是:3+(30-1)×2;
(2)分子、分母依次增加2,所以第100个数的分子是:1+(100-1)×2;分母是:2+(100-1)×2;
(3)分子依次增加1,所以第10个分数的分子是10,分母的第一个因数是1、3、5、7、^11…;第二个因数是3、5、7、9、11…;第一个因数比第二个因数大2,所以第10个分数的分母的第一个因数是19,第二个因数是19+2=21.
(4)由所给算式得出:这个加法算式的和等于这个算式中加数的个数的平方数,再写成两个相同因数乘积的形式即可;
因为50×50,说明这个算式里有50个加数,根据第50个加数=1+(50-1)×2计算出第50个加数即可.
点评:解决本题的关键是找出规律,再利用规律写数.
(1)3,5,7,9,11…61;(第30个);
(2)
 ,
, ,
, ,
, ,
, ,
, ,…
,… (第100个);
(第100个);(3)
 ,
,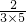 ,
,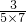 ,
,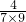 ,
,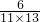 ,
,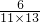 …
…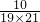 (第10个);
(第10个);(4)1=1=1×1
1+3=4=2×2
1+3+5+7=16=4×4
1+3+5+7+9+11+13=49=7×7;
1+3+5+7+9+11+13+…99=2500=50×50.
故答案为:(1)61;(2)
 ;(3)
;(3)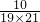 ;(4)49,7,7;99,2500.
;(4)49,7,7;99,2500.分析:(1)数列中的数依次增加2,所以第30个数是:3+(30-1)×2;
(2)分子、分母依次增加2,所以第100个数的分子是:1+(100-1)×2;分母是:2+(100-1)×2;
(3)分子依次增加1,所以第10个分数的分子是10,分母的第一个因数是1、3、5、7、^11…;第二个因数是3、5、7、9、11…;第一个因数比第二个因数大2,所以第10个分数的分母的第一个因数是19,第二个因数是19+2=21.
(4)由所给算式得出:这个加法算式的和等于这个算式中加数的个数的平方数,再写成两个相同因数乘积的形式即可;
因为50×50,说明这个算式里有50个加数,根据第50个加数=1+(50-1)×2计算出第50个加数即可.
点评:解决本题的关键是找出规律,再利用规律写数.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 去框右面这个数表里的数,每次框出5个数.一共可以
去框右面这个数表里的数,每次框出5个数.一共可以 下面是一个乘法算式,式中“偶”字表示偶数(0、2、4、6、8),“奇”字表示奇数(1、3、5、7、9),请写出这个算式.
下面是一个乘法算式,式中“偶”字表示偶数(0、2、4、6、8),“奇”字表示奇数(1、3、5、7、9),请写出这个算式.