题目内容
用  去框右面这个数表里的数,每次框出5个数.一共可以
去框右面这个数表里的数,每次框出5个数.一共可以
(1)如果这5个数的和是130,应该怎么框?
(2)能框出和是140的5个数吗?为什么?
 去框右面这个数表里的数,每次框出5个数.一共可以
去框右面这个数表里的数,每次框出5个数.一共可以15
15
个不同的和.(1)如果这5个数的和是130,应该怎么框?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 |
11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 |
分析:用一个正方形框子框出的5个数的和必定是框子中间的数的5倍;数表中边缘的行和列的数字不能再框中间,只能是中间的3行5列共15个数字在框中间,一个数对应一个框,就得到一个和;
(1)如果这5个数的和是130,用130除以5,就得到框中间的数26;
(2)用140除以5,得到28,28在数表的最后一列,不能在框的中间,因此得解.
(1)如果这5个数的和是130,用130除以5,就得到框中间的数26;
(2)用140除以5,得到28,28在数表的最后一列,不能在框的中间,因此得解.
解答:解:框出的最小5个数是2、8、9、10、16,2+8+9+10+16=45=9×5,…
框出最大的5个数是20、26、27、28、34,20+26+27+28+34=27×5=135;
一共可以有3×5=15个不同的和;
(1)130÷5=26,所以框出的5个数是19、25、26、27、33;
(2)140÷5=28,28在数表的边缘,不能在框中间,所以不能框出;
框出最大的5个数是20、26、27、28、34,20+26+27+28+34=27×5=135;
一共可以有3×5=15个不同的和;
(1)130÷5=26,所以框出的5个数是19、25、26、27、33;
(2)140÷5=28,28在数表的边缘,不能在框中间,所以不能框出;
点评:先找到规律,再根据规律求解.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
用形如 正方形去框右面这个数表里的数,每次框出4个数,一共可以框出________个不同的和;如果框出的4个数之和是88,这4个数中最大的一个数是________.
正方形去框右面这个数表里的数,每次框出4个数,一共可以框出________个不同的和;如果框出的4个数之和是88,这4个数中最大的一个数是________.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 |
 正方形去框右面这个数表里的数,每次框出4个数,一共可以框出
正方形去框右面这个数表里的数,每次框出4个数,一共可以框出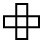 去框右面这个数表里的数,每次框出5个数,一共可以框出
去框右面这个数表里的数,每次框出5个数,一共可以框出