题目内容
 下面是一个乘法算式,式中“偶”字表示偶数(0、2、4、6、8),“奇”字表示奇数(1、3、5、7、9),请写出这个算式.
下面是一个乘法算式,式中“偶”字表示偶数(0、2、4、6、8),“奇”字表示奇数(1、3、5、7、9),请写出这个算式.分析:本题要据数和的奇偶性进行分析,因为已知积的千位和十位分别为3、5,所以可从这两个数入手进行分析,奇+偶=3,说明前边数相加不可能出现进一情况,1+2=2,即被乘数与乘数个位相乘积的百位是1,则被乘数的百位与乘数的个位一定是1,被乘数与乘数十位相乘积的十位是2,1×2=2由此可知,被乘数十位是1,乘数十位是2,(因为积为4位数且千位是偶数,所以不可能是7和6,3和4、8和9),那么被乘数与乘数个位相乘积的十位是1,1+4=5,则被乘数与乘数个位相乘积的个位是4,2×2=4,则被乘数的个位为 2,由此得出此算式为:1112×21;
解答:解:本题要据数和的奇偶性进行分析:
因为已知积的千位和十位分别为3、5,奇+偶=3,前边数相加不可能出现进一情况,
1+2=2,即被乘数与乘数个位相乘积的百位是1,则被乘数的百位与乘数的个位一定是1,被乘数与乘数十位相乘积的十位是2;
1×2=2由此可知,被乘数十位是1,乘数十位是2,(因为积为4位数且千位是偶数,所以不可能是7和6,3和4、8和9);
那么被乘数与乘数个位相乘积的十位是1,1+4=5,则被乘数与乘数个位相乘积的个位是4;
2×2=4,则被乘数的个位为 2.
由此得出此算式为:1112×21.
故答案为:
因为已知积的千位和十位分别为3、5,奇+偶=3,前边数相加不可能出现进一情况,
1+2=2,即被乘数与乘数个位相乘积的百位是1,则被乘数的百位与乘数的个位一定是1,被乘数与乘数十位相乘积的十位是2;
1×2=2由此可知,被乘数十位是1,乘数十位是2,(因为积为4位数且千位是偶数,所以不可能是7和6,3和4、8和9);
那么被乘数与乘数个位相乘积的十位是1,1+4=5,则被乘数与乘数个位相乘积的个位是4;
2×2=4,则被乘数的个位为 2.
由此得出此算式为:1112×21.
故答案为:
| |||||||
| 1 1 2 |
| 2 2 4 |
| 2 3 5 2 |
点评:完成本题要了解数的奇偶性的基础上,细心分析数据,找到突破口就好解答了.

练习册系列答案
相关题目
 在下面乘法算式中,每一方框要填一个数字,若一个汉字代表一个数字,不同汉字代表不同的数字.请问最后的积(五位数)是多少?
在下面乘法算式中,每一方框要填一个数字,若一个汉字代表一个数字,不同汉字代表不同的数字.请问最后的积(五位数)是多少?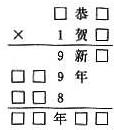 在下面乘法算式中,每一个方框里要填一个数字;每一个汉字代表一个数字,不同的汉字代表不同的数字,相同的汉字代表相同的数字,那么,这个乘法算式的最后乘积是
在下面乘法算式中,每一个方框里要填一个数字;每一个汉字代表一个数字,不同的汉字代表不同的数字,相同的汉字代表相同的数字,那么,这个乘法算式的最后乘积是