题目内容
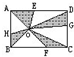 如图,长方形AB=7厘米,BC=10厘米,AE=CF=4厘米,DG=BH=3厘米.求阴影部分的面积.
如图,长方形AB=7厘米,BC=10厘米,AE=CF=4厘米,DG=BH=3厘米.求阴影部分的面积.分析:根据题干,就是要求出阴影部分4个三角形的面积之和,令△OAE的AE边上的高是H,△OFC的FC边上的高为h,如图:S△OAE+S△OFC=
×AE×H+
×FC×h=
×4×(H+h),根据长方形的性质可得H+h=AB=7厘米;所以:S△OAE+S△OFC=
×4×7=14(平方厘米);同理S△OBH+S△ODG=
×3×10=15(平方厘米),由此可以求出阴影部分的面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:阴影部分的面积为:
(S△OAE+S△OFC)+(S△OBH+S△ODG),
=
×4×7+
×3×10,
=14+15,
=29(平方厘米),
答:阴影部分的面积是29平方厘米.
(S△OAE+S△OFC)+(S△OBH+S△ODG),
=
| 1 |
| 2 |
| 1 |
| 2 |
=14+15,
=29(平方厘米),
答:阴影部分的面积是29平方厘米.
点评:此题抓住相对的两个三角形的高的和正好是长方形的一个边长,是求得阴影部分面积的关键.

练习册系列答案
相关题目
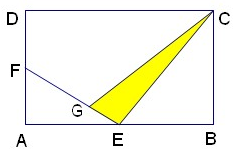 如图,ABCD为长方形,AB=10厘米,BC=6厘米,E、F分别为AB、AD中点,且FG=2GE.则阴影部分的面积等于
如图,ABCD为长方形,AB=10厘米,BC=6厘米,E、F分别为AB、AD中点,且FG=2GE.则阴影部分的面积等于 如图,ABCD是个长方形,BCFE是个正方形,AB为10厘米,BC为4厘米,P为AD边上任意一点.图中阴影部分的面积是
如图,ABCD是个长方形,BCFE是个正方形,AB为10厘米,BC为4厘米,P为AD边上任意一点.图中阴影部分的面积是 (2007?慈溪市)列式计算.
(2007?慈溪市)列式计算.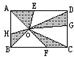 如图,长方形AB=7厘米,BC=10厘米,AE=CF=4厘米,DG=BH=3厘米.求阴影部分的面积.
如图,长方形AB=7厘米,BC=10厘米,AE=CF=4厘米,DG=BH=3厘米.求阴影部分的面积.